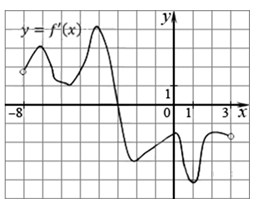
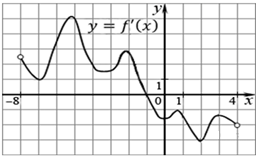
На рисунке изображен график производной функции f (x), определенной на интервале (–8; 3). В какой точке отрезка [–3; 2] функция f (x) принимает наибольшее значение?

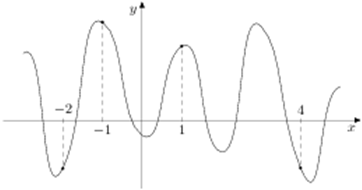
На рисунке изображен график функции y = f (x) и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

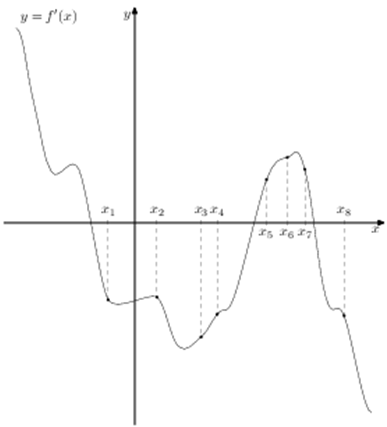
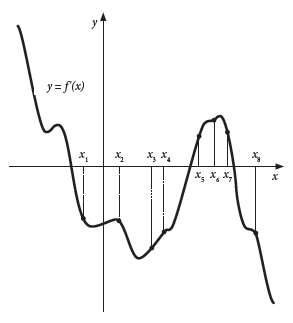
На рисунке изображён график y = f′ (x) производной функции f (x) и восемь точек на оси абсцисс: x₁, x₂, x₃, …, x_S. В скольких из этих точек функция f (x) убывает?

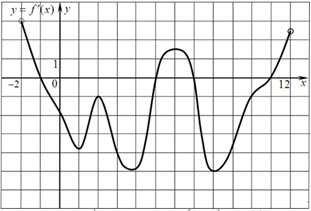
На рисунке изображен график производной функции f (x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f (x). В ответе укажите длину наибольшего из них.

На рисунке изображен график производной функции f (x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.

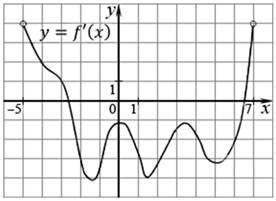
На рисунке изображен график производной функции f (x), определенной на интервале (–18; 6). Найдите абсциссу точки минимума функции f (x) на отрезке [–13; 1].

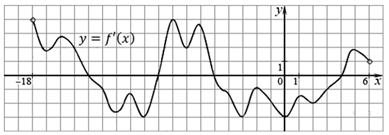
На рисунке изображен график производной функции f (x), определенной на интервале (−7; 14). Найдите абсциссу точки максимума функции f (x) на отрезке [−6; 9].

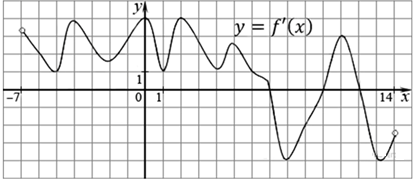
На рисунке изображен график производной функции f (x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.

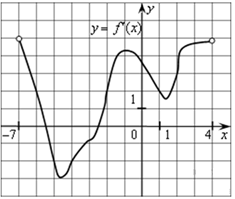
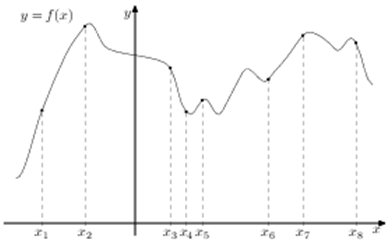
На рисунке изображён график функции y = f (x) и восемь точек на оси абсцисс: x₁, x₂, x₃, …, x_S. В скольких из этих точек производная функции f (x) положительна?

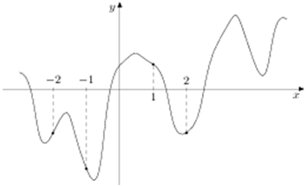
На рисунке изображен график функции y = f (x) и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

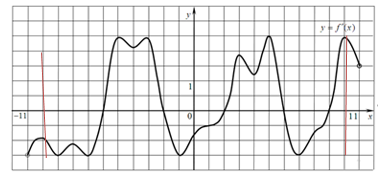
На рисунке изображен график производной функции f (x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f (x) на отрезке [−10; 10].

На рисунке изображен график производной функции f (x), определенной на интервале (–8; 4). В какой точке отрезка [–7; –3]

f (x) принимает наименьшее значение.

На рисунке изображен график производной функции f (x), определенной на интервале (−4; 8). Найдите точку экстремума функции f (x) на отрезке [−2; 6].

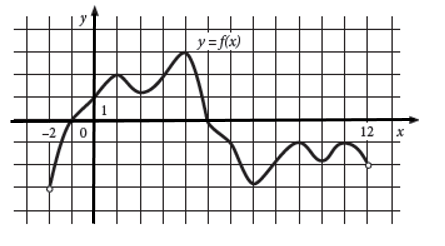
На рисунке изображен график функции f (x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f (x) равна 0.

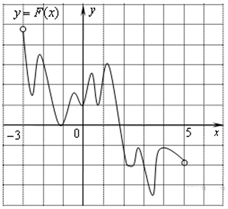
На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f (x), определённой на интервале (−3; 5). Пользуясь рисунком, определите количество решений уравнения f (x) = 0 на отрезке [−2; 4].

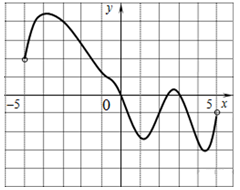
На рисунке изображен график функции y = f(x), определенный на интервале (-2;12). Найдите сумму точек экстремума функции f(x).

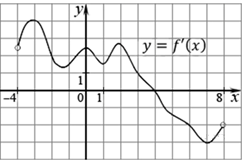
На рисунке изображен график y = f’(x) - производной функции f(x), определенный на интервале (-8;3). В какой точке отрезка [-3;2] функция f(x) принимает наибольшее значение?

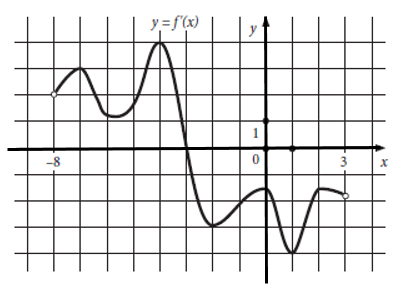
На рисунке изображен график y = f’(x) — производной функции f(x) и восемь точек на оси абсцисс: х₁, х₂, х₃… х₈. В скольких из этих точек функция f(x) возрастает?