а) Решим уравнение, применяя формулы приведения:

sinx + sinx + 2sin²x = $\displaystyle\frac{3}{2} \Leftrightarrow$

2sinx + 2sin²x = $\displaystyle\frac{3}{2} \Leftrightarrow$

4sin²x + 4sinx − 3 = 0.

Пусть sinx = t, |t| ≤ 1.

Получим систему:

$\left\{\begin{aligned}&4t^2+4t-3=0\\&|t|\le1\end{aligned}\right. \Leftrightarrow$

$\left\{\begin{aligned}&\left[\begin{aligned}&t_1=-1.5\\&t_2={\small\frac{1}{2}}\end{aligned}\right.\\&|t|\le1\end{aligned}\right. \Rightarrow$

t = $\displaystyle\frac{1}{2} \Leftrightarrow$

sinx = $\displaystyle\frac{1}{2} \Rightarrow$

x = (−1)^k$\,\displaystyle\frac{\pi}{6}$ + πk, k ϵ $\mathbb{Z}$.

Результат решения этого уравнения разложим на два составляющих решения:

$\left[\begin{aligned}&x=\displaystyle\frac{\pi}{6}+2\pi n,\;n\in\mathbb{Z},\\[2pt]&x=\frac{5\pi}{6}+2\pi m,\;m\in\mathbb{Z}.\end{aligned}\right.$

б) Каждое из этих решений должно находиться на промежутке $\left[-\displaystyle\frac{\pi}{2};\pi\right]$.

−$\displaystyle\frac{\pi}{2}$ ≤ $\displaystyle\frac{\pi}{6}$ + 2πn ≤ π $\Leftrightarrow$

−$\displaystyle\frac{2}{3}$π ≤ 2πn ≤ $\displaystyle\frac{5}{6}$π $\Leftrightarrow$

− $\displaystyle\frac{1}{3}$ ≤ n ≤ $\displaystyle\frac{5}{12}$, n = 0.

При n = 0, получим $\displaystyle\frac{\pi}{6}$.

−$\displaystyle\frac{\pi}{2}$ ≤ $\displaystyle\frac{5\pi}{6}$ + 2πm ≤ π $\Leftrightarrow$

−$\displaystyle\frac{4}{3}$π ≤ 2πm ≤ $\displaystyle\frac{1}{6}$π $\Leftrightarrow$

−$\displaystyle\frac{4}{6}$ ≤ m ≤ $\displaystyle\frac{1}{12}$, m = 0.

При m = 0 получим x = $\displaystyle\frac{5\pi}{6}$.

а) Преобразуем уравнение:

4sinx·cosx – 4cosx + sinx – 1 = 0;

4cosx·(sinx – 1) + (sinx – 1) = 0;

(sinx – 1)·(4cosx + 1) = 0;

$\left[\begin{aligned}&\sin x - 1 = 0\\&4\cos x + 1 = 0\end{aligned}\right.$

Получаем: sinx = 1 или cosx = −$\displaystyle\frac{1}{4}$, откуда x = $\displaystyle\frac{\pi}{2}$ + 2πk, или x = ±arccos$\left(-\displaystyle\frac{1}{4}\right)$ + 2πk, k ϵ $\mathbb{Z}$.

б) С помощью числовой окружности отберем корни на отрезке $\left[\displaystyle\frac{\pi}{2};\frac{3\pi}{2}\right]$, в данной задаче это можно сделать визуально без каких−либо дополнительных расчётов:

Заданному интервалу принадлежат корни:

$\displaystyle\frac{\pi}{2}$, arccos$\left(-\displaystyle\frac{1}{4}\right)$, 2π − arccos$\left(-\displaystyle\frac{1}{4}\right)$.

а) Используем формулу приведения:

cos$\left(\displaystyle\frac{3\pi}{2}+2x\right)$ = cosx.

Напомним, что можно обойтись без понятия формулы приведения, расписав косинус суммы двух углов и подставив в полученное выражение значения функций синус и косинус в точке $\displaystyle\frac{3\pi}{2}$.

2sinx·cosx = cosx, теперь вынесем общий множитель за скобку:

sin2x = cosx;

2sinx·cosx = cosx;

2sinx·cosx – cosx = 0;

cosx·(2sinx – 1) = 0.

Тогда cosx = 0 или sinx = $\displaystyle\frac{1}{2}$.

Решая cosx = 0 получим: x = $\displaystyle\frac{\pi}{2}$ + πk, k ϵ $\mathbb{Z}$.

Решая sinx = $\displaystyle\frac{1}{2}$ получим: x = $\displaystyle\frac{\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$ или x = $\displaystyle\frac{5\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$.

Таким образом: x = $\displaystyle\frac{\pi}{2}$ + πk, x = $\displaystyle\frac{\pi}{6}$ + 2πk, x = $\displaystyle\frac{5\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$.

б) С помощью единичной окружности отберём корни на отрезке $\left[\displaystyle\frac{5\pi}{2};4\pi\right]$.

Находим: $\displaystyle\frac{5\pi}{2},\,\frac{17\pi}{6},\,\frac{7\pi}{2}$.

Без расчётов, визуально сходу определить корни принадлежащие отрезку может далеко не каждый, нужна серьёзная практика, поэтому покажем безошибочный способ отбора корней, которым советуем пользоваться: переведём радианы в градусы. Так как π радиан это 180º, то отрезок $\left[\displaystyle\frac{5\pi}{2};4\pi\right]$ будет выглядеть следующим образом: [450º; 720º]. Отберём корни, подставляя значения k в полученное решение уравнения:

При k = 1:

x = $\displaystyle\frac{\pi}{2}$ + π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{2\pi}{2}$ = $\displaystyle\frac{3\pi}{2}$ = 270º;

x = $\displaystyle\frac{\pi}{6}$ + 2π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{12\pi}{6}$ = $\displaystyle\frac{13\pi}{6}$ = 390º;

x = $\displaystyle\frac{5\pi}{6}$ + 2π = $\displaystyle\frac{5\pi}{6}$ + $\displaystyle\frac{12\pi}{6}$ = $\displaystyle\frac{17\pi}{6}$ = 510º.

При k = 2:

x = $\displaystyle\frac{\pi}{2}$ + 2π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{4\pi}{2}$ = $\displaystyle\frac{5\pi}{2}$ = 450º;

x = $\displaystyle\frac{\pi}{6}$ + 4π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{24\pi}{6}$ = $\displaystyle\frac{25\pi}{6}$ = 750º;

x = $\displaystyle\frac{5\pi}{2}$ + 4π = $\displaystyle\frac{5\pi}{2}$ + $\displaystyle\frac{24\pi}{6}$ = $\displaystyle\frac{29\pi}{6}$ = 870º.

При k = 3:

x = $\displaystyle\frac{\pi}{2}$ + 3π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{6\pi}{2}$ = $\displaystyle\frac{7\pi}{2}$ = 630º;

x = $\displaystyle\frac{\pi}{6}$ + 6π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{36\pi}{6}$ = $\displaystyle\frac{37\pi}{6}$ = 1100º;

x = $\displaystyle\frac{5\pi}{6}$ + $\displaystyle\frac{36\pi}{6}$ = $\displaystyle\frac{41\pi}{6}$ = 1230º.

При k = 4: проверять корни нет смысла, так как видно, что результат будет лежать вне пределов интервала: x = $\displaystyle\frac{\pi}{2}$ + 4π > 720º.

Отрезку [450º; 720º] принадлежат корни 390º; 450º; 510º, в радианах это $\displaystyle\frac{5\pi}{2},\,\displaystyle\frac{17\pi}{6},\,\displaystyle\frac{7\pi}{2}$. Ответ можно записывать либо в градусах, либо радианах, значения не имеет.

Преобразуем уравнение:

$\displaystyle\frac{\cos x}{\sin x}$·2sinx·cosx – (1 – cos2x) = 0 $\;\Leftrightarrow\;$ 2cos²x – 2sin²x = 0 $\;\Leftrightarrow\;$ cos2x = 0 $\;\Rightarrow$

2x = $\displaystyle\frac{\pi}{2}$ + πn, n ϵ $\mathbb{Z}$;

x = $\displaystyle\frac{\pi}{4}$ + $\displaystyle\frac{\pi}{2}$n, n ϵ $\mathbb{Z}$.

0 < $\displaystyle\frac{\pi}{4}$ + $\displaystyle\frac{\pi}{2}$n < π $\;\Leftrightarrow\;$ −1/4 < n/2 < 3/4 $\;\Leftrightarrow\;$ −1/2 < n < 3/2, n = 0,1 $\;\Leftrightarrow$

При n = 0, получим x = $\displaystyle\frac{\pi}{4}$, а при n = 1 получим $\displaystyle\frac{3\pi}{4}$.

а) Преобразуем выражение, используя свойства степеней

$7^{\,2\sin x}=7^{\sqrt{2}\sin 2x}$

$2\sin x=\sqrt{2}\sin 2x$

Перенесем все слагаемые влево, воспользуемся формулой синуса двойного угла и вынесем повторяющийся элемент за скобки:

$\sqrt{2}\sin 2x - 2\sin x = 0$

$2\sqrt{2}\sin x \cos x - 2\sin x = 0$

$\sin x (\sqrt{2}\cos x - 1) = 0$

Произведение равно нулю, когда хотя бы один из множителей равен 0:

$\sin x = 0$ или $\cos x = \frac{\sqrt{2}}{2}$

$ x = \pi k, k ϵ \mathbb{Z}$;

$ x = \frac{\pi}{4} + 2\pi k, k ϵ \mathbb{Z}$;

$ x = -\frac{\pi}{4} + 2\pi k, k ϵ \mathbb{Z}$.

б) Отметим корни на числовой окружности и выделим необходимый промежуток

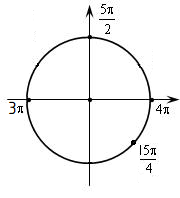
Необходимому отрезку принадлежат корни:

$\displaystyle\ 3\pi$, $\displaystyle\ 4\pi$, $\displaystyle\frac{15\pi}{4}$.

а) Преобразуем выражение, используя свойства степеней

$\large 5^{2\sqrt{3}\cos\left(x+\textstyle\frac{3\pi}{2}\right)}=5^{-2\cos(x+\pi)}$

$2\sqrt{3}\cos\left(x+\displaystyle\frac{3\pi}{2}\right)=-2\cos(x+\pi)$

Перенесем слааемые в левую части и используем формулы приведения:

$2\sqrt{3}\sin x-2\cos x=0$

Получили однородное уравнение первой степени. Разделим на cosx ≠ 0 (cosx ≠ 0, ибо, в противном случае, из уравнения следует, что и sinx = 0, что невозможно, так как тогда не будет выполняться основное тригонометрическое тождество sin²x + cos²x =1).

$\mathop{\mathrm{tg}}x = \displaystyle\frac{1}{\sqrt{3}}$

$x=\displaystyle\frac{\pi}{6}+\pi k,\,k\in\mathbb{Z}$

б) Построим график функции тангенс и определим корни, принадлежащие промежутку.

Видно, что нужный корень располагается в 3 периоде, то есть $\,x=4\pi+\displaystyle\frac{\pi}{6}=\frac{25\pi}{6}$.

а) Преобразуем выражение, используя свойства логарифма

Пусть $\cos x = t,\,-1\le t\le1$.

Тогда

$2t^2+3t-2=0 \\[5pt] D=9+16=25 \\[3pt] t=\displaystyle\frac{-3\pm5}{4} \\ \left[\begin{aligned}&\vphantom{\Bigl{|}}t=-2\,<-1,\,не\ подходит\\&t=\displaystyle\frac{1}{2}\end{aligned}\right. \\[10pt] \cos x = \displaystyle\frac{1}{2} \\[10pt] x=\pm\displaystyle\frac{\pi}{3}+2\pi k,\,k\in\mathbb{Z}$

б) Построим график косинуса и определим корни в промежутке $\left[-\displaystyle\frac{7\pi}{2};-2\pi\right]$.

Единственный корень в промежутке – ближайший корень левее чем $-2\pi$.

$x=-2\pi-\displaystyle\frac{\pi}{3}=-\displaystyle\frac{7\pi}{3}$

а) Преобразуем выражение, используя свойства логарифма

$\cos x = -\displaystyle\frac{\sqrt{2}}{2} \\ x = \pm \displaystyle\frac{3\pi}{4} + 2\pi k,\,k\in\mathbb{Z}$

б) Построим график косинуса и определим корни в промежутке $\left[-2\pi;-\displaystyle\frac{\pi}{2}\right]$.

Первый корень получается движением от $-2\pi$ вправо, то есть $x=-2\pi+\displaystyle\frac{3\pi}{4}=-\displaystyle\frac{5\pi}{4}$, а второй движением от 0 влево $x=0-\displaystyle\frac{3\pi}{4}=-\displaystyle\frac{3\pi}{4}$.

а) Преобразуем выражение, используя свойства степеней

$(2^x)^{2}-8\!\cdot\!2^x+15=0$

б) Так как основание логарифма больше 1, то данная функция возрастает.

$\log_23<\log_24=2<\log_25$, поэтому корень $\log_23$ не попадает в нужный промежуток.

Заметим, что $9<10\Rightarrow3<\sqrt{10}$

$\log_25<\log_28=3<\sqrt{10}$

а) Преобразуем выражение, используя свойства степеней

$(3^x)^3-5\!\cdot\!(3^x)^2-9\!\cdot\!3^x+45=0$

Сгруппируем слагаемые

Произведение равно 0, если хотя бы один из множителей равен 0.

б) Так как основание логарифма больше 1, то данная функция возрастает.

$1=\log_33<\log_34<\log_35<\log_310\,$ и $\,x=1$ не попадает в нужный интервал.

а) Преобразуем выражение, используя свойства логарифма

$x^2-14x=32 \\ x^2-14x-32=0$

По теореме Виета

$\left[\begin{aligned}&x=-2\\&x=16\vphantom{\bigl(}\end{aligned}\right.$

б) Так как основание логарифма больше 1, то данная функция возрастает.

Приведём к одному основанию.

$-2=\log_3\displaystyle\frac{1}{9}=\log_3\frac{10}{90} \\[1pt] \log_30.1=\log_3\displaystyle\frac{1}{10}=\log_3\frac{9}{90}$

Откуда:

$-2=\log_3\displaystyle\frac{10}{90}>\log_3\frac{9}{90}=\log_30.1$

Очевидно, что -2 меньше $5\sqrt{10}$.

Тогда корень (-2) входит в промежуток.

Заметим, что , то есть левая граница данного в условии промежутка отрицательная. Корень 16 – положительное число, значит, оно явно больше левой границы.

Сравним 16 и $5\sqrt{10}$

$\begin{aligned}16&\vee5\sqrt{10}\\256&\vee25\!\cdot\!10\\256&\vee250\\256&>250 \Rightarrow 16>5\sqrt{10},\ тогда\ корень\ 16\ не\ входит\ в\ промежуток.\end{aligned}$

а) Отметим, что выражение √2sin2x ≥ 0, так как |cosx + sinx| имеет неотрицательное значение, поэтому sin2x ≥ 0.

Используя свойство модуля, получим два отдельных уравнения, решения каждого из них будут являться решением данного уравнения:

cosx + sinx = √2sin2x или –(cosx + sinx) = √2sin2x.

Решаем cosx + sinx = √2sin2x.

Возводим в квадрат обе части:

(cosx + sinx)² = 2sin²2x;

cos²x + 2cosx·sinx + sin²x = 2sin²2x;

2sin²2x − sin2x – 1 = 0.

Решая квадратное уравнение, получим: sin2x = 1 и sin2x = $-\displaystyle\frac{1}{2}$.

Так как sin2x ≥ 0 (это область допустимых значений), то второе уравнение решать нет смысла.

Решаем sin2x = 1, получим:

2x = $\displaystyle\frac{\pi}{2}$ + 2πn, n ϵ $\mathbb{Z}$ $\;\mathbf{\Biggl|}\cdot\displaystyle\frac{1}{2}$;

x = $\displaystyle\frac{\pi}{4}$ + πn, n ϵ $\mathbb{Z}$.

Решением уравнения –(cosx + sinx) = √2sin2x является тот же корень, так как при возведении в квадрат обеих частей получим то же уравнение.

б) Сделаем отбор корней на данном в условии промежутке , используя метод двойного неравенства.

Для этого подставим найденный в пункте а) корень x = $\displaystyle\frac{\pi}{4}$ + πn, n ϵ $\mathbb{Z}$ в промежуток, а затем учтем, что n может быть только целым числом.

В этот промежуток входят только два целых значения n – это n=3 и 4.

Подставим их в изначальный корень.

$x=\displaystyle\frac{\pi}{4}+\pi\!\cdot\!4=\frac{\pi+16\pi}{4}=\frac{17\pi}{4} \\[15pt] x = \displaystyle\frac{\pi}{4}+\pi\!\cdot\!3=\frac{\pi+12\pi}{4}=\frac{13\pi}{4}$