


0
из 6Решил заданий
0
из 6Не решил заданий
6
из 6Осталось заданий
Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие "буква" - "цифра" должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Угол между скрещивающимися прямыми, между прямой и плоскостью
6 заданийВ правильном тетраэдре АВСD точка К – середина ВD, точка М – середина ВС. Найдите угол между прямыми АК и DМ.
1) Дополнительное построение: пусть точка L – середина ВМ. Тогда KL – средняя линия треугольника ВDМ; значит, KL||DM, и потому искомый угол есть $\varphi=\angle AKL$.
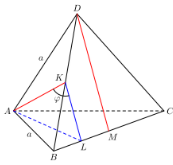
Величину $\varphi$ мы вычислим по теореме косинусов из треугольника $AKL$. Предварительно найдём стороны этого треугольника.
Из треугольника АВD находим АК как высоту в равностороннем треугольнике:
$AK=\displaystyle\frac{a\sqrt{3}}{2}$, где a – ребро тетраэдра.
Кроме того, $KL=\displaystyle\frac{1}{2}DM=\frac{1}{2}\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}$.
Остаётся найти сторону АL. Это можно сделать из треугольника АВL, в котором АВ=а, ВL= $\displaystyle\frac{a}{4}$, $\angle ABL=60^{\circ}$. По теореме косинусов получим:
$AL^2=AB^2+BL^2-2\cdot AB\cdot BL\cdot \cos ABL \\[5pt] AL^2=a^2+\displaystyle\frac{a^2}{16}-2\cdot a\cdot \frac{a}{4}\cdot \frac{1}{2}=\frac{17a^2}{16}-\frac{a^2}{4}=\frac{13a^2}{16} \\[7pt] AL = \displaystyle\frac{a\sqrt{13}}{4}$
Теперь возвращаемся к треугольнику АКL. По теореме косинусов:
$AL^2=AK^2+KL^2-2\cdot AK\cdot AL\cdot \cos\varphi$
Подставляем найденные длины сторон:
$\displaystyle\frac{13a^2}{16}=\frac{a^2\!\cdot\! 3}{4}+\frac{a^2\!\cdot\! 3}{16}-2\cdot\frac{a\sqrt{3}}{2}\cdot\frac{a\sqrt{3}}{4}\cdot \cos\varphi \\[10pt] \displaystyle\frac{13a^2}{16}=\frac{3a^2}{4}+\frac{3a^2}{16}-\frac{3a^4}{4}\cdot\cos\varphi \\[10pt] \displaystyle\frac{a^2}{8}=\frac{3a^2}{4}\cdot\cos\varphi \\[10pt] \cos\varphi=\displaystyle\frac{1}{6}$
Тогда искомый угол – это $\arccos\displaystyle\frac{1}{6}$.
Площадь боковой поверхности прямоугольного параллелепипеда АВСDА1В1С1D1 равна $6\sqrt{15}$, AB = $\sqrt{5}$, AA1 = $\sqrt{3}$. Вычислите угол между плоскостью В1ВD и прямой СD1.
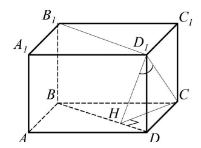
$Проведём\ CH\!\perp\!BD.\ Поскольку\ DD_1\!\perp\!ABC\ и\ CH\!\subset\!ABC,\,то\ DD_1\!\perp\!CH.\\Таким\ образом,\,CH\ перпендикулярен\ двум\ пересекающимся\ прямым,\,BD\,\,и\ DD_1,\,лежащим\ в\\плоскости\ B_1BD,\,а,\,значит,\,является\ перпендикуляром\ к\ этой\ плоскости.\ Тогда\ CD_1\ -\\наклонная,\,а\ D_1H\ -\ её\ проекция\ на\ эту\ плоскость,\,и\ углом\ между\ прямой\ CD_1\ и\ плоскостью\\B_1BD\ является\ угол\ CD_1H.$
$\begin{aligned}S_{бок}=2S_{AA_1B_1B}+2S_{AA_1D_1D}=2(AB+AD)\cdot\, &AA_1=2\left(\sqrt{5}+BC\right)\cdot\sqrt{3}=6\sqrt{15};\\[3pt]BC=2\sqrt{5}.&\ \end{aligned}$
По теореме Пифагора из треугольника BCD получим $BD^2=BC^2+CD^2$, откуда BD = 5.
Тогда
$CH=\displaystyle\frac{BC\cdot CD}{BD}=\frac{2\sqrt{5}\cdot\sqrt{5}}{5}=2$
По теореме Пифагора из треугольника $CDD_1$ получим $CD_1^2=CD^2+DD_1^2$, откуда $CD_1=2\sqrt{2}$.
Из прямоугольного треугольника $CHD_1$ получим:
$\sin\angle CD_1H=\displaystyle\frac{CH}{CD_1}=\frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2}},$
Значит, $\angle CD_1H=45^{\circ}$.
В правильной треугольной призме ABCA1B1C1 боковое ребро равно стороне основания. Найдите угол между прямой АА1 и плоскостью АВС1.
Угол между прямой и плоскостью не изменится при параллельном сдвиге прямой. Поскольку СС1 параллельна АА1, искомый угол $\varphi$ есть угол между прямой СС1 и плоскостью АВС1.
Пусть М - середина АВ, пусть АВ=а. Проведём высоту СН в треугольнике СС1М. Покажем, что СН - перпендикуляр к плоскости АВС1. Для этого нужно предъявить две пересекающиеся прямые этой плоскости, перпендикулярные СН.
Первая прямая очевидна - это С1М. В самом деле, $CH\!\perp\! C_1M$ по построению.
Вторая прямая — это АВ. Действительно, проекцией наклонной СН на плоскость AВC служит прямая СМ; при этом $AB\!\perp\! CM$. Из теоремы о трёх перпендикулярах следует тогда, что $AB\!\perp\! CH$.
Итак, $CH\!\perp\! ABC_1$.
Стало быть, угол между СС1 и АВС1 есть $\varphi=\angle CC_1H=\angle CC_1M$.
Имеем:
$CM=\displaystyle\frac{a\sqrt{3}}{2} \\ По\ теореме\ Пифагора\ найдём\ C_1M\colon \\ C_1M=\sqrt{CC_1^2+CM^2}=\displaystyle\sqrt{a^2+a^2\!\cdot\!{\small\frac{3}{4}}}=\sqrt{\small\frac{a^2\,7}{4}}=\displaystyle\frac{a\sqrt{7}}{2} \\ \sin CC_1M=\displaystyle\frac{MC}{MC_1}=\frac{a\sqrt{3}}{2}:\frac{a\sqrt{7}}{2}=\sqrt{\frac{3}{7}} \\ Значит,\ сам\ угол\ равен\ \arcsin\sqrt{\displaystyle\frac{3}{7}}$
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 8 и BC = 6. Длины боковых рёбер пирамиды $SA=\sqrt{21},\,SB=\sqrt{85},\,SD=\sqrt{57}$.
а) Докажите, что $SA$ — высота пирамиды.
б) Найдите угол между прямыми $SC$ и $BD$.
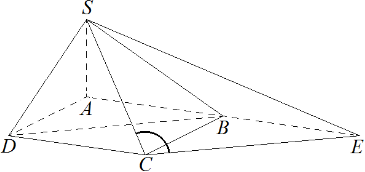
а) В треугольнике $SAB$ имеем:
$SD^2=57=21+36=SA^2+AD^2$,
поэтому треугольник $SAB$ прямоугольный с гипотенузой $SB$ и прямым углом $SAB$. Аналогично, из равенства
$SD^2=57=21+36=SA^2+AD^2$
получаем, что $\angle SAD=90^{\circ}$. Так как прямая $SA$ перпендикулярна прямым $AB$ и $AD$ прямая $SA$ перпендикулярна плоскости $ABD$ по признаку перпендикулярности прямой и плоскости.
б) Дополнительное построение: на прямой отметим такую точку E, что BDCE — параллелограмм, тогда $BE=DC=AB\;\,и\;DB = CE$. Найдём угол SCE. По теореме Пифагора:
$\quad AC=BD=\sqrt{AB^2+AD^2}=10;\ SC=\sqrt{SA^2+AC^2}=11\;и\;SE^2=SA^2+AE^2=277. \\ По\ теореме\ косинусов\colon \\[3pt] \begin{aligned}\qquad SE^2=SC^2+CE^2-2SC\cdot CE&\cdot\cos\angle SCE;\ 277=121+100-220\cos\angle SCE; \\ &\cos\angle SCE = -\displaystyle\frac{14}{55}.\end{aligned}$
Искомый угол равен $\arccos\displaystyle\frac{14}{55}$.
В правильной шестиугольной пирамиде SABCDEF с вершиной S боковые рёбра равны 2, а сторона основания – 1.
а) Докажите, что плоскость, проходящая через вершину S и середины рёбер AF и СD перпендикулярна основанию.
б) Найдите косинус угла между прямой АС и плоскостью SAF.
а) Проведем эту плоскость. Так как, плоскость проходит через середины ребер К и N , на отрезке KN будет лежать центр правильного шестиугольника О. Значит, отрезок SO будет являться высотой правильной шестиугольной пирамиды. Значит, по признаку перпендикулярности плоскостей плоскость SKN будет перпендикулярна плоскости основания.
б) Так как пирамида правильная, то KN будет параллельно АС. Значит, искомый угол – угол между KN и SAF. Точнее возьмем отрезок ОК.
ОК перпендикулярно FA, так как в основании правильный шестиугольник.
SK перпендикулярно AF, так как треугольник AFS равнобедренный (по свойству равнобедренного треугольника о том, что медиана является высотой).
Значит, AF перпендикулярно плоскости KSO, а значит, перпендикулярно любой прямой, лежащей в этой плоскости.
Проведем отрезок ОН перпендикулярно SK.
ОН перпендикулярно SK. AF перпендикулярно ОН, значит, по признаку перпендикулярности прямой и плоскости ОН перпендикулярно плоскости ASF, то есть, точка Н является проекцией точки О на плоскость SAF.
Точка К проецируется в саму себя. Значит, угол между плоскостью ASF и прямой ОК – угол ОКН.
Найдем SK. Треугольник SAF – равнобедренный, значит, $SA=2, AK=0,\!5$. Тогда SK по теореме Пифагора будет равно: $SK=\displaystyle\sqrt{4-{\small\frac{1}{4}}}=\frac{\sqrt{15}}{2}$.
ОК – высота в равностороннем треугольнике AFO, значит, $OK=\displaystyle\frac{\sqrt{3}}{2}$.
Тогда найдем косинус угла OKS по определению тригонометрической функции:
$\cos OKS=\displaystyle\frac{OK}{KS}=\frac{\sqrt{3}}{2}:\frac{\sqrt{15}}{2}=\frac{1}{\sqrt{5}}.$
В основании четырехугольной пирамиды MABCD лежит прямоугольник ABCD со сторонами $AB=\displaystyle\sqrt{11} $ и $BC=\displaystyle\ 2\sqrt{3} $. Длины боковых рёбер пирамиды $MA=5, MB=6, MD=\sqrt{37}$.
а) Докажите, что MA – высоты пирамиды.
б) Найдите угол между прямой MC и плоскостью AMB.
а) По определению, высота – это перпендикуляр, опущенный из вершины пирамиды на противоположную плоскость.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Рассмотрим треугольник MAB:
$6^2=5^2+\displaystyle\sqrt{11}^2$, тогда
$MB^2=AB^2+AM^2$
Тогда по теореме, обратной теореме Пифагора, угол MAB – прямой.
Рассмотрим треугольник MAD:
$\displaystyle\sqrt{37}^2=5^2+\left(2\sqrt{3}\right)^2,\,тогда \\ MD^2=AD^2+AM^2$
Тогда по теореме, обратной теореме Пифагора, угол MAD – прямой.
Прямая MA перпендикулярна двум пересекающимся прямым AB и AD, лежащим в плоскости основания, значит, перпендикулярна и всей этой плоскости.
Тогда MA – высота пирамиды, что и требовалось доказать.
б) Из того факта, что MA- высота, следует, что эта прямая перпендикулярна плоскости основания и любой прямой, лежащей в этой плоскости, в том числе прямой BC.
Также BC перпендикулярна AB, так как в основании пирамиды лежит прямоугольник.
Тогда прямая BC перпендикулярна двум пересекающимся прямым AB и MA, лежащим в плоскости AMB, значит, перпендикулярна и всей этой плоскости.
Тогда MC – наклонная, BC – перпендикуляр, а MB – проекция.
Угол между прямой MC и плоскостью AMB – это угол между прямой MC и её проекцией MB на эту плоскость, откуда угол CMB – искомый.
Рассмотрим треугольник CMB.
Угол CBM – прямой, так как CB перпендикулярно плоскости AMB.
$\mathop{\mathrm{tg}} CMB=\displaystyle\frac{2\sqrt{3}}{6}=\displaystyle\frac{\sqrt{3}}{3}$
Откуда угол CMB составляет 30˚.

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

«Выбери тест, предмет и нажми кнопку «Начать решать»

После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию

Решай задания и записывай ответы. После 1-ой попытки ты сможешь посмотреть решение

Сбоку ты можешь посмотреть статистику и прогресс по предмету

Нажми, чтобы начать решать вариант. Как только ты перейдешь на страницу, запустится счетчик времени, поэтому подготовь заранее все, что может тебе понадобиться

Отмечай те статьи, что прочитал, чтобы было удобнее ориентироваться в оглавлении

Ты прошел обучение! Теперь ты знаешь как пользоваться сайтом и можешь переходить к решению заданий