


0
из 8Решил заданий
0
из 8Не решил заданий
8
из 8Осталось заданий
Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие "буква" - "цифра" должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Угол между плоскостями
8 заданийВ правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые рёбра равны 3. На ребре AA1 отмечена точка E так, что AЕ:ЕA1 = 2:1. Найдите угол между плоскостями ABC и BED1.
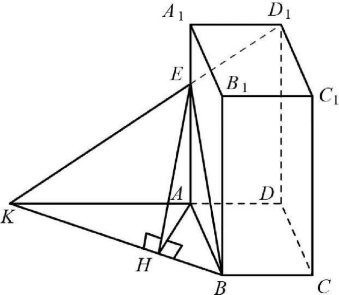
1) Прямая D1E пересекает прямую АD в точке К. Плоскости АВС и ВЕD1 пересекаются по прямой КВ.
Из точки Е опустим перпендикуляр ЕН на прямую КВ, тогда отрезок АН (проекция ЕН) перпендикулярен прямой КВ по теореме о трех перпендикулярах. Угол АНЕ является линейным углом двугранного угла, образованного плоскостями АВС и ВЕD1.
2) Поскольку АЕ:ЕА1 = 2:1, получаем:
$AE=\displaystyle\frac{2AA_1}{3}=2;\;EA_1=AA_1-AE=1.$
Из подобия по двум углам треугольников A1D1E и AKE находим:
$AK=\displaystyle\frac{AE}{EA_1}\cdot A_1D_1=2.$
В прямоугольном треугольнике AKB с прямым углом A:
AB =1; AK=2;
$BK=\displaystyle\sqrt{AB^2+AK^2}=\sqrt{5}$,
откуда высота
$AH=\displaystyle\frac{AK\cdot AB}{BK}=\frac{2\sqrt{5}}{5}.$
Из прямоугольного треугольника AHE с прямым углом A получаем:
$\mathop{\mathrm{tg}}\angle AHE=\displaystyle\frac{AE}{AH}=\sqrt{5}$.
Значит, сам угол – это $\mathop{\mathrm{arctg}}\sqrt{5}$.
Основание прямой четырехугольной призмы ABCDA1В1C1D1 - прямоугольник ABCD, в котором AB=5, AD=$\displaystyle\sqrt{11}$. Найдите угол между плоскостью основания призмы и плоскостью, проходящей через середину ребра AD перпендикулярно прямой BD1, если расстояние между прямыми AС и B1D1 равно $2\sqrt{3}$. Ответ дайте в градусах.
Расстояние между прямыми AС и B1D1 равно расстоянию между основаниями, то есть высоте призмы. Значит, высота призмы равна $2\sqrt{3}$.
Угол между плоскостями равен углу между прямыми, перпендикулярными этим плоскостям.
Поэтому искомый угол равен углу между ребром DD1 и прямой BD1.
Рассмотрим треугольник BDD1. Его катеты равны DD1=$2\sqrt{3}$, по теореме Пифагора $BD=\displaystyle\sqrt{AB^2+AD^2}=6$.
Значит, $\angle BD_1D=\mathop{\mathrm{arctg}\displaystyle\frac{6}{2\sqrt{3}}}=\mathop{\mathrm{arctg}}\sqrt{3}=60^{\circ}$.
В правильной треугольной пирамиде SABC с основанием ABC точка M - середина ребра SA, точка K - середина ребра SB. Найдите угол между плоскостями CMK и ABC, если SC=6, AB=4.
Проведем перпендикуляр CQ к MK, Q - середина MK. Из точки Q опустим перпендикуляр QP на плоскость основания. Точка P лежит на медиане CL треугольника ABC. Прямая MK параллельна прямой пересечения плоскостей CMK и ABC, QP$\perp\!$ MK и CQ$\perp\!$ MK. Следовательно, $\small\angle$QCP - линейный угол искомого угла двугранного угла. Найдем QP.
$SO=\displaystyle\sqrt{SC^2-CO^2}=\sqrt{6^2-\left({\textstyle\frac{4\cdot\sqrt{3}}{3}}\right)^2}=\sqrt{6^2-\small\frac{16}{3}}=2\sqrt{\small\frac{23}{3}}; \\ QP=\displaystyle\frac{1}{2}SO=\sqrt{\small\frac{23}{3}}; \\[13pt] CP=\displaystyle\frac{5}{6}CL=\frac{5}{3}\sqrt{3}.$
Значит:
$\mathop{\mathrm{tg}}\angle QCP=\displaystyle\frac{\sqrt{23}\cdot\sqrt{3}}{\sqrt{3}\cdot 5}=\displaystyle\frac{\sqrt{23}}{5}$.
В правильной четырёхугольной пирамиде SABCD с основанием ABCD точка M - середина ребра SA , точка K - середина ребра SC. Найдите угол между плоскостями BMK и ABC, если AB = 4, SC = 7.
Проведём из точки B перпендикуляр BQ к MK, Q - середина MK. Точка Q является серединой высоты SO. Прямая MK параллельна прямой пересечения плоскостей, QB$\,\perp\,$MK, OB$\,\perp\,$MK. Следовательно, $\small\angle$QBO - линейный угол искомого угла. Найдём QO.
$BO=2\displaystyle\sqrt{2};\ SO=\sqrt{SB^2-OB^2}=\sqrt{7^2-(2\sqrt{2})^2}=\sqrt{49-8\vphantom{\small(}}=\sqrt{41}; \\[8pt] QO=\displaystyle\frac{1}{2}SO=\frac{\sqrt{41}}{2}$
Значит,
$\mathop{\mathrm{tg}}\angle QBO=\displaystyle\frac{\sqrt{41}}{4\sqrt{2}}=\displaystyle\frac{\sqrt{82}}{8}$
В правильной треугольной призме АВСА1В1С1, все рёбра которой равны 1, найдите косинус угла между плоскостями АСВ1 и ВА1С1.
Пусть DE — линия пересечения данных плоскостей, F — середина отрезка DE, G — середина отрезка A1С1. Угол GFB1 является линейным утлом между данными плоскостями. В треугольнике GFB1 имеем:
GB1= $\displaystyle\frac{\sqrt{3}}{2}$, как высота в равностороннем треугольнике.
В треугольнике АВ1С DE – средняя линия, значит, $DE=\displaystyle\frac{1}{2}AC=\frac{1}{2}.\ DF=\frac{1}{4}$.
$B_1D=\displaystyle\frac{1}{2}AB_1=\frac{1}{2}\cdot\sqrt{2}=\frac{\sqrt{2}}{2}$.
Тогда FB1 найдем по теореме Пифагора:
$FB_1=\displaystyle\sqrt{B_1D^2-DF^2}=\sqrt{\small\frac{2}{4}-\frac{1}{16}}=\sqrt{\small\frac{7}{16}}=\frac{\sqrt{7}}{4}$
Аналогично найдем FG.
FG = FB1 = $\displaystyle\frac{\sqrt{7}}{4}$.
По теореме косинусов находим
$GB_1^{\,2}=FG^{\,2}+FB_1^{\,2}-2\cdot FG\cdot EB_1\cdot\cos GFB_1 \\ \displaystyle\frac{3}{4}=\frac{7}{16}+\frac{7}{16}-2\cdot\frac{\sqrt{7}}{4}\cdot\frac{\sqrt{7}}{4}\cdot\cos GFB_1 \\ \cos\angle GFB_1=\displaystyle\frac{1}{7}.$
Дана правильная четырёхугольная призма ABCDA1B1C1D1 стороны основания равны 1, а боковые рёбра равны 5. На ребре AA1 отмечена точка E так, что AE : EA1 = 2 : 3.
а) Постройте двугранный угол между плоскостями ABC и BED1.
б) Найдите угол между плоскостями ABC и BED1.
1) Дополнительное построение.
Прямая D1E пересекает прямую AD в точке K.
Плоскости ABC и BED1 пересекаются по прямой KB.
Из точки E опустим перпендикуляр EH на прямую KB.
$\left.\begin{gathered}EA\perp ABC\rightarrow EA\perp BK \\ EH\perp BK \\ BK\in ABC\end{gathered}\right\}\rightarrow\displaystyle{{\small(по\ ТТП)}\atop AH\perp BK} \\[25pt] \left.\begin{gathered}AH\perp BK \\ AH\in ABC \\ EH\perp BK \\ EH\in BED_1\end{gathered}\right\}\rightarrow\angle(BED_1;ABC)=\angle EHA\ -\ искомый\ угол$
Угол AHE является линейным углом двугранного угла, образованного плоскостями ABC и BED1.
2) Поскольку AE : EA1 = 2 : 3, получаем:
$AE=\displaystyle\frac{2AA_1}{5}=2,\ EA_1=AA_1-AE=3.$
Из подобия треугольников A1D1E и AKE находим:
$AK=\displaystyle\frac{AE}{EA_1}\cdot A_1D_1=\frac{2}{3}$.
В прямоугольном треугольнике AKB с прямым углом A:
$\displaystyle AB=1;\ AK=\frac{2}{3}; \\ BK=\displaystyle\sqrt{AB^2+AK^2}=\frac{\sqrt{13}}{3},\ откуда\ высота\colon \\ AH=\displaystyle\frac{AK\cdot AB}{BK}=\frac{2\sqrt{13}}{13}.$
Из прямоугольного треугольника AHE с прямым углом A получаем:
$\mathop{\mathrm{tg}}\angle AHE=\displaystyle\frac{AE}{AH}=\sqrt{13}.$
В правильной треугольной призме ABCA1В1С1 боковое ребро равно стороне основания. Точка К — середина ребра ВВ1. Найдите угол между плоскостями А1КС и ABC. Ответ дайте в градусах.
Пусть L - точка пересечения прямых А1К и АВ. Тогда плоскость А1КС пересекает плоскость АВС по прямой CL.
Треугольники А1В1К и KBL равны по катету и острому углу. Следовательно, равны и другие катеты: А1В1=BL.
Рассмотрим треугольник ACL. В нём ВА = ВС = BL . Угол CBL равен 120°, стало быть, $\angle$BCL=30°. Кроме того, $\angle$ВСА=60°. Поэтому $\angle ACL=\angle BCA+\angle BCL=90^{\circ}$
Итак, LC$\,\perp\,$AC. Но прямая АС служит проекцией прямой А1С на плоскость АВС. Пo теореме о трёх перпендикулярах заключаем тогда, что LC$\,\perp\,$A1C.
Таким образом, угол А1СА — линейный угол двугранного угла, образованного полуплоскостями А1КС и АВС. Это и есть искомый угол. Из равнобедренного прямоугольного треугольника AlAC мы видим, что он равен 45°.
В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 2, точка М – середина ребра АВ, точка О – центр основания пирамиды, точка F делит отрезок SO в отношении 3:1, считая от вершины пирамиды.
а) Докажите, что прямая MF перпендикулярна прямой SC.
б) Найдите угол между плоскостью MBF и плоскостью АВС.
а)
1) $O\in CM$, так как СМ – медиана и высота в равностороннем треугольнике.
$\rightarrow$ FM лежит в плоскости SCM.
Продлим прямую MF до пересечения с прямой SC.
Пусть $MF\cap SC=K$.
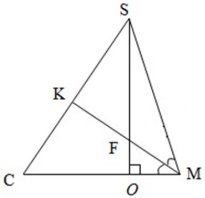
SM и – медианы равных равносторонних треугольников со стороной
$2\rightarrow SM=CM=\displaystyle\frac{a\sqrt{3}}{2}=\sqrt{3}$
2) Точка О – центр основания, значит, $\displaystyle\frac{CO}{OM}=\frac{2}{1}.\ Тогда\ CO=\frac{2}{3}\!\cdot\!\sqrt{3},\ а\ OM=\frac{1}{3}\!\cdot\!\sqrt{3}$.
Найдем по теореме Пифагора из треугольника SMO:
$SM^2=SO^2+OM^2 \\[5pt] 3=SO^2+\displaystyle\frac{3}{9} \\[5pt] \displaystyle SO=\sqrt{3-{\small\frac{3}{9}}}=\sqrt{{\small\frac{24}{9}}}=\displaystyle\frac{2}{3}\sqrt{6}$
3) По условию, точка F делит отрезок SO в отношении 3:1, считая от вершины пирамиды. Таким образом,
$SF=\displaystyle\frac{3}{4}SO=\frac{3}{4}\cdot\frac{2}{3}\sqrt{6}=\frac{\sqrt{6}}{2},\ а\ FO=\frac{1}{4}\cdot\frac{2}{3}\sqrt{6}=\frac{\sqrt{6}}{6}$.
4) Треугольник FMO – прямоугольный. Найдем FM по теореме Пифагора:
$FM=\displaystyle\sqrt{FO^2+OM^2}=\sqrt{{\small\frac{6}{36}}+{\small\frac{3}{9}}}=\sqrt{\small\frac{18}{36}}=\sqrt{\small\frac{1}{2}}=\frac{1}{\sqrt{2}}$
Докажем, что $\angle OMF=\angle SMF$. Если эти углы будут равны, то тогда KM – биссектриса в равнобедренном треугольнике, проведенная к основанию, а, значит, будет являться высотой $\rightarrow MK\perp SC$.
Если косинусы углов $\angle OMF$ и $\angle SMF$ будут равны, то будут равны и сами углы.
$\cos\angle OMF=\displaystyle\frac{OM}{FM}=\frac{\sqrt{3}}{3}:\frac{1}{\sqrt{2}}=\frac{\sqrt{6}}{3}$
Косинус угла $\angle SMF$ найдем по теореме косинусов:
$SF^2=SM^2+FM^2-2\cdot SM\cdot FM\cdot\cos\angle SMF \\[8pt] \displaystyle\frac{6}{4}=3+\frac{1}{2}-2\cdot\sqrt{3}\cdot\frac{1}{\sqrt{2}}\cdot\cos\angle SMF \\ -2=-2\cdot\displaystyle\frac{\sqrt{3}}{\sqrt{2}}\cos\angle SMF \\[5pt] \cos\angle OMF=\displaystyle\frac{OM}{FM}=\frac{\sqrt{3}}{3}:\frac{1}{\sqrt{2}}=\frac{\sqrt{6}}{3}$
Что и требовалось доказать.
б)
1) По условию и доказанному в пункте а) мы имеем:
$\begin{gathered}OF\perp ABC \\ OM\perp AB \\ OM\in ABC\end{gathered}\rightarrow\displaystyle{\small (по\ теореме\ о\ трёх\ перпендикулярах)\atop\normalsize FM\perp AB\quad\,}$
Таким образом, $\angle(ABC;FMB)=\angle(FM;OM)=\angle OMF$.
2) По доказанному в пункте а) мы имеем:
$\cos\angle OMF=\displaystyle\frac{\sqrt{6}}{3},\ тогда\ \angle OMF=\arccos\frac{\sqrt{6}}{3}$.

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

«Выбери тест, предмет и нажми кнопку «Начать решать»

После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию

Решай задания и записывай ответы. После 1-ой попытки ты сможешь посмотреть решение

Сбоку ты можешь посмотреть статистику и прогресс по предмету

Нажми, чтобы начать решать вариант. Как только ты перейдешь на страницу, запустится счетчик времени, поэтому подготовь заранее все, что может тебе понадобиться

Отмечай те статьи, что прочитал, чтобы было удобнее ориентироваться в оглавлении

Ты прошел обучение! Теперь ты знаешь как пользоваться сайтом и можешь переходить к решению заданий