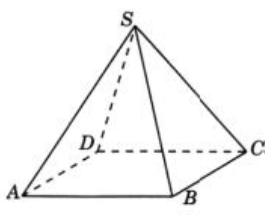
Первый способ

Прямая ВС параллельна плоскости SАD, в которой лежит прямая SА. Следовательно, расстояние между скрещивающимися прямыми SА и ВС равно расстоянию от прямой ВС до плоскости SАD или от любой точке прямой ВС до плоскости SAD.

Возьмем точку В.

Найдем искомое расстояние методом двойного выражения объемов.

$V_{BASD}=\displaystyle\frac{1}{3}\cdot S_{ABD}\cdot h_{пирамиды}=\frac{1}{3}\cdot S_{SAD}\cdot h$, где h – искомое расстояние.

Найдем высоту пирамиды:

Рассмотрим треугольник $SBD.\ SD=SB=1.\ BD=\sqrt{2}$, как диагональ квадрата со стороной 1.

Треугольник SBD – прямоугольный, так как $SD^2+SB^2=BD^2$.

Высота в треугольнике SBD – высота пирамиды.

Значит, $h_{пирамиды}=\displaystyle\frac{ab}{c}=\frac{1\cdot1}{\sqrt{2}}=\frac{1}{\sqrt{2}}.$

Подставим все данные, чтобы найди искомое расстояние:

$h=\displaystyle\frac{S_{ABD}\cdot h_{пирамиды}}{S_{SAD}}=\frac{\frac{1}{2}\cdot AB\cdot AD\cdot h_{пирамиды}}{\frac{AD^2\sqrt{3}}{4}}=\frac{\frac{1}{2}\cdot1\cdot1\cdot\frac{1}{\sqrt{2}}}{1\cdot\frac{\sqrt{3}}{4}}=\frac{\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3}$

Второй способ

Прямая ВС параллельна плоскости SАD, в которой лежит прямая SА. Следовательно, расстояние между скрещивающимися прямыми SА и ВС равно расстоянию от прямой ВС до плоскости SАD.

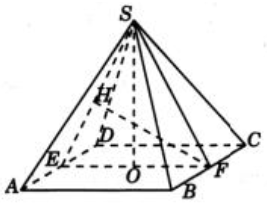
Пусть Е и F соответственно середины рёбер АD и ВС. Тогда искомым перпендикуляром будет высота FН треугольника SEF. В треугольнике SEF имеем:

EF=1, SE=SF=$\displaystyle\frac{\sqrt{3}}{2}$, высота SO равна $\displaystyle\frac{\sqrt{2}}{2}$. Для площади S треугольника SEF имеют место равенства $2S=EF\cdot SO=SE\cdot FH$, из которых получаем $FH=\displaystyle\frac{\sqrt{6}}{3}$.

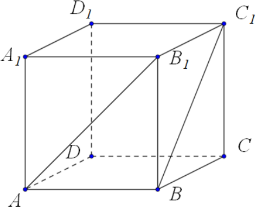
Первый способ

Прямая ВС₁ параллельна плоскости B₁AD₁ при признаку параллельности прямой и плоскости.

Значит, расстояние между исходными прямыми равно расстоянию от любой точки прямой ВС₁ до плоскости B₁AD₁. Возьмем точку В.

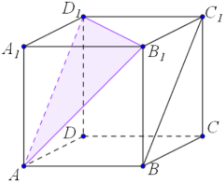
Найдем это расстояние методом двойного выражения объёмов.

$V_{B_1D_1AB}=\displaystyle\frac{1}{3}\cdot S_{ABB_1}\cdot A_1D_1=\frac{1}{3}\cdot S_{AB_1D_1}\cdot h$, h – искомое расстояние.

$h=\displaystyle\frac{S_{ABB_1}\cdot A_1D_1}{S_{AB_1D_1}}=\frac{\frac{1}{2}\cdot AB\cdot BB_1\cdot A_1D_1}{\frac{AB_1^{\,2}\sqrt{3}}{4}}=\frac{\frac{1}{2}\cdot1\cdot1\cdot1}{2\cdot\frac{\sqrt{3}}{4}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$

Второй способ

Плоскости AB₁D₁ и BDC₁, в которых лежат данные прямые, параллельны. Следовательно, расстояние между этими скрещивающимися прямыми равно расстоянию между соответствующими плоскостями.

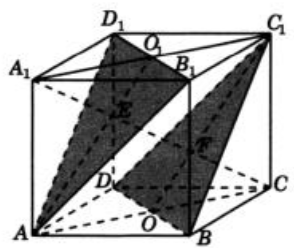
Диагональ СА₁ куба перпендикулярна этим плоскостям (А₁Е высота в пирамиде А₁AB₁D₁, аналогично с BDC₁) . Обозначим Е и F как точки пересечения диагонали СА₁ соответственно с плоскостями AB₁D₁ и BDC₁. Длина отрезка EF будет равна расстоянию между прямыми АВ₁ и ВС₁. Пусть О и O₁ соответственно центры граней ABCD и A₁B₁C₁D₁ куба. В треугольнике АСЕ отрезок OF параллелен АЕ и проходит через середину АС. Следовательно, OF — средняя линия треугольника АСЕ и, значит, EF = FC. Аналогично доказывается, что O₁Е — средняя линия треугольника A₁C₁F и, значит, А₁Е = EF. Таким образом, EF составляет одну треть диагонали CA₁, т. е. EF=$\displaystyle\frac{\sqrt{3}}{3}$.

Дополнительное построение: SO – высота пирамиды.

Пусть Е - основание перпендикуляра, опущенного из точки О на ребро SA.

$\begin{gathered}BD\perp AC \\ BD\perp SO \\ AC\cap SO=O\end{gathered}\Rightarrow BD\perp AOS$ (по признаку перпендикулярности прямой и плоскости)

Значит, ВО перпендикулярно любой прямой, лежащей в плоскости ASO $\rightarrow BO\perp OE$.

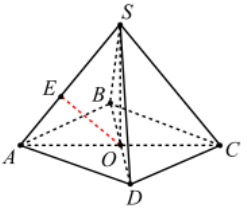
Таким образом, ОЕ - общий перпендикуляр к скрещивающимся прямым ВD и SA .

Найдем его длину как высоту ОЕ, опущенную на гипотенузу AS треугольника AOS.

$AO=\displaystyle\frac{1}{2}AC=\frac{1}{2}\cdot\sqrt{2}=\frac{\sqrt{2}}{2}$

AS = 1

Найдем SO по теореме Пифагора:

$SO^2=AS^2-AO^2=1-\displaystyle\frac{2}{4}=\frac{2}{4} \\ SO=\displaystyle\frac{\sqrt{2}}{2} \\ h=\displaystyle\frac{ab}{c}=\frac{AO\cdot OS}{AS}=\frac{\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{2}}{2}}{1}=\frac{2}{4}=\frac{1}{2}=0,\!5$

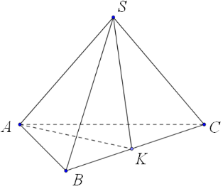
а) Точка К – середина ВС, значит, SK и АК – медианы в треугольниках SBC и АВС.

Эти треугольники по условию равнобедренные, значит, что SK и АВС – высоты в треугольниках SBC и АВС.

$\left.\begin{gathered}SK\perp BC \\ AK\perp BC \\ SK\cap AK=K\end{gathered}\right\}\rightarrow BC\perp AKS\ {(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)} \\[20pt] \left.\begin{gathered}BC\perp AKS \\ BC\in ABC\end{gathered}\right\}\rightarrow AKS\perp ABC\ {(по\ признаку\atop перпендикулярности\ плоскостей)}$

Что и требовалось доказать.

б) Дополнительное построение: пусть КН перпендикулярно прямой AS.

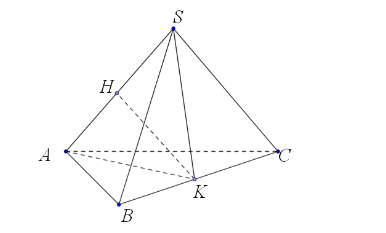
Тогда мы имеем:

$\left.\begin{gathered}KH\perp BC\ (по\ доказанному\ в\ пункте\ а)\!\!\!\!\! \\ KH\perp AS\ (по\ построению)\end{gathered}\right\}\rightarrow KH\ -\ общий\ перпендикуляр\ к\ скрещивающимся\ прямым\ SA\ и\ BC$

КН – высота в равнобедренном треугольнике AKS. Найдем боковые стороны в этом треугольнике.

$SC=10;\ KC=\displaystyle\frac{1}{2}BC=6$

Тогда найдем SK по теореме Пифагора:

$SK^2=SC^2-KC^2=100-36=64$

SK=8

SH=AH=6

SK=8

Тогда найдем КН по теореме Пифагора:

$KH^2=SK^2-SH^2=64-36=28 \\[8pt] KH=2\sqrt{7}$

а) Сечение призмы — квадрат AA₁ML. Тогда диагонали перпендикулярны: $AM\perp A_1L$.

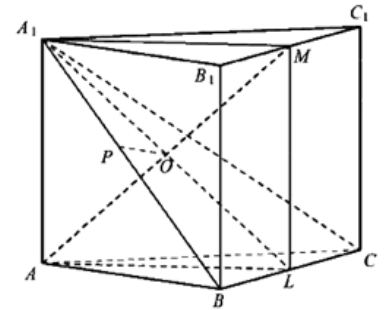
$\left.\begin{gathered}AL\perp BC\ (по\ свойству\ равнобедренного\ треугольника)\!\!\!\!\!\!\!\!\!\! \\ ML\perp BC\ (так\ как\ призма\ прямая)\end{gathered}\right\}\rightarrow AM\perp BC\ {(по\ теореме\ о\atop трёх\ перпендикулярах)} \\[15pt] \left.\begin{gathered}AM\perp BC \\ AM\perp A_1L\end{gathered}\right\}\rightarrow{(по\ признаку\ перпендикулярности\ прямой\ и\ плоскости)\atop\displaystyle AM\perp A_1BC\;}$

Что и требовалось доказать.

б) Из точки О опустим перпендикуляр ОР на прямую А₁В.

$OP\!\perp\! A_1B$ (по построению) и $OP\!\perp\! AM$ (так как АМ перпендикулярно плоскости А₁ВС), следовательно, ОР – общий перпендикуляр для прямых АМ и А₁В.

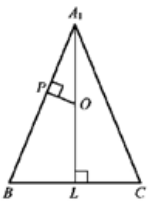
Сторона квадрата AA₁ML равна высоте треугольника ABC, то есть:

$h_{равностороннего\ треугольника}=\displaystyle\frac{a\sqrt{3}}{2}=\frac{2\sqrt{7}\!\cdot\!\sqrt{3}}{2}=\sqrt{21}=AL$

Диагональ квадрата AA₁ML $A_1L=\sqrt{42}$. В равнобедренном треугольнике A₁BC основание $BC=2\sqrt{7}$, боковая сторона $A_1B=7$. Отсюда, используя подобие треугольников A₁OP и A₁BL найдем

$OP=\displaystyle\frac{A_1O\cdot LB}{A_1B}=\frac{A_1L\cdot BC}{4A_1B}=\frac{\sqrt{42}\cdot2\sqrt{7}}{4\cdot7}=\frac{\sqrt{6}}{2}$

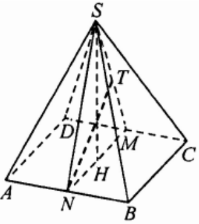
а) 1) В основании четырехугольной пирамиды лежит квадрат. Точки M и N является серединами противоположных сторон квадрата, значит, они перпендикулярны сторонам АВ и CD и параллельны AD и ВС.

Тогда:

$\left.\begin{gathered}CD\perp NM\ (по\ доказанному) \\ CD\perp SM\ (по\ св\!-\!ву\ равнобедренного\ треугольника)\!\!\!\!\!\!\!\!\!\!\! \\ NM\cap SM=M\end{gathered}\right\}\rightarrow\begin{gathered}\begin{smallmatrix}(по\ теореме\ о\ перпендикулярности \\ прямой\ и\ плоскости)\end{smallmatrix} \\ CD\perp SNM\end{gathered}$

2) Точка Т лежит на SM, потому что по-нашему с вами построению проведем NT перпендикулярно SM, тогда:

$\left.\begin{gathered}NT\perp SM\ (по\ построению) \\ CD\perp NT\ (по\ доказанному\ в\ п.1)\end{gathered}\right\}\rightarrow NT\ -\ перпендикулярно\ SCD.$

3) Рассмотрим треугольник SNM и найдем длину каждой стороны.

$SN^2=NH^2+SH^2=3+9=12 \\[8pt] SN=2\sqrt{3}$

SN равно SM как апофемы в правильной пирамиде.

$NM=AD=BC=2\sqrt{3}$

Имеем, что треугольник SNM – равносторонний, значит, каждая его высота является медианой, а NT – высота.

Что и требовалось доказать.

б) 1) Пусть Е – основание перпендикуляра, опущенного из точки Т на прямую SC.

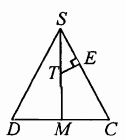
Прямая NT перпендикулярна прямой ТЕ, так как NT – высота пирамиды NCSD.

$\left.\begin{aligned}TE&\perp SC \\ TE&\perp NT\end{aligned}\right\}\rightarrow TE\ -\ общий\ перпендикуляр\ к\ скрещивающимся\ прямым\ SC\ и\ NT$

ТЕ – искомое расстояние.

2) Треугольники SET и SMC подобны по двум углам (один угол общий, второй угол прямой), следовательно:

$\displaystyle\frac{ET}{MC}=\frac{ST}{SC},\ откуда\ ET=\frac{ST\cdot CM}{SC}=\frac{SM}{2}\cdot\frac{CD}{2}\cdot\frac{1}{SC}$

SC по теореме Пифагора будет равно:

$SC^2=SM^2+MC^2=12+3=15 \\[8pt] SC=\sqrt{15} \\[3pt] ET=\displaystyle\frac{SM}{2}\cdot\frac{CD}{2}\cdot\frac{1}{SC}=\sqrt{3}\cdot\sqrt{3}\cdot\frac{1}{\sqrt{15}}=\frac{3}{\sqrt{15}}=\frac{\sqrt{15}}{5}$