


0
из 8Решил заданий
0
из 8Не решил заданий
8
из 8Осталось заданий
Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие "буква" - "цифра" должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Объемы, площади, сечения
8 заданийНайдите площадь сечения, вершинами которого являются вершина А и середины рёбер ВВ1 и DD1единичного куба АВСDA1B1C1D1.
Дополнительное построение К – середина ребра ВВ1 и М – середина ребра DD1.
Строим сечение методом следов:
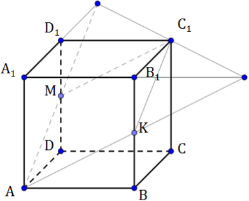
Сечением является ромб. Найдем его сторону по теореме Пифагора:
$AK^2=AB^2+KB^2=1+\displaystyle\frac{1}{4}=\frac{5}{4} \\ AK=\displaystyle\frac{\sqrt{5}}{2}$
Большая диагональ куба является диагональю куба – АС1.
$AC_1=\sqrt{3}$
Найдем угол АКС1 по теореме косинусов:
$AC_1^2=AK^2+KC_1^2-2\cdot AK\cdot KC_1\cdot\cos AKC_1 \\[5pt] 3=\displaystyle\frac{5}{4}+\frac{5}{4}-2\cdot\frac{5}{4}\cdot\cos AKC_1 \\[2pt] \cos AKC_1=-\displaystyle\frac{1}{5}$
Тогда синус AKС1 равен $\displaystyle\frac{2\sqrt{6}}{5}$.
Найдем площадь искомого сечения:
$S=AK\cdot KC_1\cdot\sin AKC_1=\displaystyle\frac{\sqrt{5}}{2}\cdot\frac{\sqrt{5}}{2}\cdot\frac{2\sqrt{6}}{2}=\frac{\sqrt{6}}{2}$.
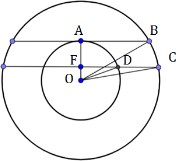
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная плоскости α, касается меньшего шара, а площадь сечения этой плоскостью большего шара равна 5. Найдите площадь сечения большего шара плоскостью α.
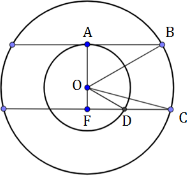
Сечение шара плоскостью – круг.
Дополнительное построение – плоскость α имеет радиус АВ, плоскость β – FD и FC.
Площадь сечения большего шара плоскостью, параллельной первоначальной плоскости, равна 5. Значит: $S=\pi R^2=\pi\cdot AB^2=5$
$AB^2=\displaystyle\frac{5}{\pi}$
Аналогичным образом найдем $FD^2=\displaystyle\frac{7}{\pi}$
Для того, чтобы найти площадь искомого сечения, надо знать, чему равно CF2.
Применим теорему Пифагора:
$OC^2=OF^2+FC^2 \\[2pt] OD^2=OF^2+FD^2$
Вычтем из одного уравнения другое.
$OC^2-OD^2=FC^2-FD^2$.
Применим еще раз теорему Пифагора:
$OA^2+AB^2=OB^2 \\[2pt] OB^2=OC^2$
Сделаем замену:
$OA^2+AB^2-OD^2=FC^2-FD^2 \\[3pt] OD=OA\rightarrow AB^2=FC^2-FD^2 \\ FC^2=AB^2+FD^2=\displaystyle\frac{5}{\pi}+\frac{7}{\pi}=\frac{12}{\pi}$
Площадь равна 12.
Также возможен случай, когда плоскости будут по одну сторону от центра. Решение будет аналогичным.
В треугольной пирамиде ABCD двугранные углы при рёбрах AD и BC равны. AB = BD = CD = AC = 5.
а) Докажите, что AD = BC.
б) Найдите объем пирамиды, если двугранные углы при AD и BC равны 60.
а)
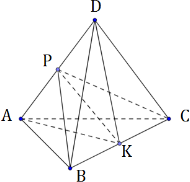
1) Дополнительное построение:
2) Треугольники АВС и АBD равнобедренные по условию, значит, АК и BP будут являться медианами по свойству равнобедренного треугольника. Тогда DK, СР также являются одновременно медианой и высотой.
Тогда ∠BPC – линейный угол двугранного угла при ребре AD, ∠AKD - линейный угол двугранного угла при ребре ВС. Из условия имеем: ∠BPC = ∠AKD.
3) РК медиана, биссектриса и высота в треугольниках ВРС и AKD. Тогда PK ⊥ BC и PK ⊥ AD.
Тогда, треугольник BPK равен треугольнику АКР по углу
$\angle BPK=\displaystyle\frac{1}{2}\angle BPC=\frac{1}{2}\angle AKD=\angle AKP$ и катету РК.
Из равенства треугольников следует, что BK = AP.
$BK=\displaystyle\frac{1}{2}BC \\[3pt] AP=\displaystyle\frac{1}{2}AD$
Следовательно, BC = AD.
б)
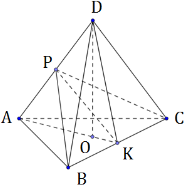
1) По данным пункта б: ∠BPC = ∠AKD = 60°, тогда треугольники АКD и ВРС равносторонние. Пусть сторона каждого такого треугольника будет равна х.
2) Дополнительное построение. Пусть DO⊥ AK.
Тогда:
$\left\{\begin{aligned}BC\perp KD\ (&по\ доказанному\ в\ пункте\ а) \\ BC\perp AK\ (&по\ доказанному\ в\ пункте\ а) \\ &KD\cap AK=K\end{aligned}\right.\!\!\!\Rightarrow BC\perp AKD\ {(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)}$
Из доказанного следует, что BC ⊥ OD. Значит:
$\left\{\begin{gathered}BC\perp OD \\ AK\perp OD \\ BC\cap AK=K\end{gathered}\right.\Rightarrow DO\perp ABC\ {(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)}$
То есть, OD – высота пирамиды.
3) AK = x по построению, тогда $BK=\displaystyle\frac{x}{2}.\ AB=5$.
Треугольник АВК прямоугольный, значит:
$AB^2=AK^2+BK^2 \\ 5^2=x^2+\left(\displaystyle\frac{x}{2}\right)^2 \\ 25={\small\displaystyle\frac{5x^2}{4}} \\[2pt] x^2=20 \\[3pt] x=2\sqrt{5}$
4) Высота пирамиды и равностороннего треугольника равна:
$OD=\displaystyle\frac{x\sqrt{3}}{2}=\frac{2\sqrt{5}\sqrt{3}}{2}=\sqrt{15}$
5) Площадь основания равна:
$S_{ABC}=\displaystyle\frac{1}{2}AK\cdot BC=\frac{1}{2}\cdot x\cdot x=\frac{1}{2}\cdot 2\sqrt{5}\cdot 2\sqrt{5}=10 \\ V=\displaystyle\frac{1}{3}\cdot h\cdot S_{ABC}=\frac{1}{3}\cdot\sqrt{15}\cdot 10=\frac{10\sqrt{15}}{3}$
В кубе $ABCDA_1B_1C_1D_1$ все рёбра равны 5. На его ребре BB1 отмечена
точка K так, что KB = 3. Через точки K и С1 проведена плоскость α, параллельная прямой BD1.
а) Докажите, что $\displaystyle\frac{A_1P}{PB_1}=\frac{1}{2}$, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.
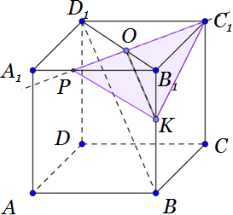
а) 1. Дополнительное построение.
Соединим вершины B1и D1. Проведем в треугольнике BB1D1 через точку К прямую, параллельную BD1.
Пусть B1D1 пересекается с построенной прямой в точке О.
Прямая BD1параллельная плоскости С1ОК, так как параллельна как минимум одной прямой ОК (по построению), лежащей в этой плоскости.
2) Через точку С1 и О проведем прямую. Пусть прямая С1О пересекается с A1B1в точке Р. Точка Р – точка пересечения плоскости α с ребром A1B1.
3) В треугольнике BB1D отрезок ОК параллелен BD1. Значит отрезок ОК делит треугольник BB1D на 2 подобных (признак подобия по 2 углам).
Значит:
$\displaystyle\frac{B_1K}{B_1B}=\frac{KO}{BD_1}=\frac{B_1O}{B_1D_1} \\[10pt] По\ условию\ BB_1=5, KB=3, значит\ B_1K=2. \\[5pt] \displaystyle\frac{B_1K}{B_1B}=\frac{2}{5}=\frac{B_1O}{B_1D_1}$
B1D1 – диагональ в квадрате. Ребро куба равно 5. Значит B1D1= $5\sqrt{2}$.
$\displaystyle\frac{2}{5}=\frac{B_1O}{B_1D_1}=\frac{B_1O}{5\sqrt{2}} \\[15pt] B_1O=2\sqrt{2}, тогда\ OD_1=B_1D_1-B_1O=3\sqrt{2}$
4) Треугольник ОС1D1подобен треугольнику ОРВ1. (подобие по 2 углам, ОС1D1= ОРВ1, так как A1B1C1D1 – квадрат, A1B1|| C1D1, секущая РС1, С1ОD1= РОВ1 как вертикальные углы)
$\begin{aligned}&\displaystyle\frac{OC_1}{OP}=\frac{OD_1}{OB_1}=\frac{C_1D_1}{PB_1} \\[6pt] &\displaystyle\frac{C_1D_1}{PB_1}=\frac{3}{2}=\frac{5}{PB_1}\end{aligned}\qquad\begin{aligned}&\displaystyle\frac{OD_1}{OB_1}=\frac{3\sqrt{2}}{2\sqrt{2}}=\frac{3}{2} \\[6pt] &PB_1=\displaystyle\frac{10}{3}\end{aligned} \\[15pt] A_1P=A_1B_1-PB_1=5-\displaystyle{\small\frac{10}{3}}={\small\frac{5}{3}}\qquad\frac{A_1P}{B_1P}=\frac{5/3}{10/3}=\frac{1}{2}$
Что и требовалось доказать.
б) Объем куба равен 125.
Объем пирамиды РВ1С1К найдем.
$V_{пирамиды}={\small\displaystyle\frac{1}{3}}S_{основания}*h$
Найдем площадь основания В1С1К.
$S=\displaystyle\frac{1}{2}2*5=5$
Ребро РВ1 перпендикулярно В1С1К, так как $ABCDA_1B_1C_1D_1$ — куб, а значит является высотой пирамиды.
$V=\displaystyle\frac{1}{3}\cdot5\cdot\frac{10}{3}=\frac{50}{9}$
Найдем объем другой части куба.
Из объема всего куба вычтем объем пирамиды.
$V=125-\displaystyle\frac{50}{9}=\frac{1075}{9}$
Основанием прямой треугольной призмы ABCA1B1C1является прямоугольный треугольник ABC с прямым углом С. Диагонали граней AA1B1B и BB1C1C равны 15 и 9 соответственно, АВ=13.
а) Докажите, что треугольник A1C1B – прямоугольный.
б) Найдите объем пирамиды AA1C1B.
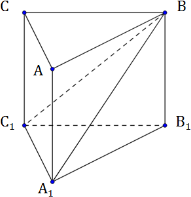
а) Угол С – прямой, значит, угол С1 тоже прямой. Тогда $A_1C_1\perp B_1C_1$.
CC1 перпендикулярно А1В1С1, так как по условию призма прямая.
$\left\{\begin{gathered}A_1C_1\perp B_1C_1 \\ CC_1\perp A_1C_1 \\ B_1C_1\cap CC_1=C_1\end{gathered}\right.\Rightarrow A_1C_1\perp B_1CC_1\ {(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)}$
Следовательно, $A_1C_1\perp BC_1$. Значит, треугольник A1BC1 - прямоугольный. Что и требовалось доказать.
б) $V_{AA_1C_1B}=\displaystyle\frac{1}{3}\cdot h\cdot S=\frac{1}{3}BC\cdot S_{AA_1C_1}$
Имеем:
$AB=13;\ AC=A_1C_1=\sqrt{A_1B^2-BC_1^2}=\sqrt{225-81}=\sqrt{144}=12$
Тогда ВС по теореме Пифагора будет равно 5.
Найдем AA1. AA1 = BB1.
По теореме Пифагора имеем:
$BB_1=\sqrt{A_1B^2-A_1B_1^2}=\sqrt{225-169\vphantom{)}}=\sqrt{56} \\ S_{AA_1C_1}=\displaystyle\frac{1}{2}A_1C_1\cdot AA_1=\frac{1}{2}\cdot12\cdot\sqrt{56}=6\sqrt{56}=12\sqrt{14} \\ V_{AA_1C_1B}=\displaystyle\frac{1}{3}\cdot h\cdot S=\frac{1}{3}BC\cdot S_{AA_1C_1}=\frac{1}{3}\cdot5\cdot12\sqrt{14}=20\sqrt{14}$
В правильной четырехугольной призме ABCDA1B1C1D1 сторона основания AB равна 6, а боковое ребро AA1 равно $4\sqrt{3}$. На ребрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причем AM= A1N = C1K =1
а) Пусть P ‐ точка пересечения плоскости MNK с ребром BC. Докажите, что MNKP ‐ квадрат
б) Найдите площадь сечения призмы плоскостью MNK.
1) Плоскость MNK пересекает параллельные плоскости ABC и A1B1C1 по параллельным прямым (построение сечения с помощью параллельных прямых), значит прямые NK и ML параллельны, причем CL также равно 1.
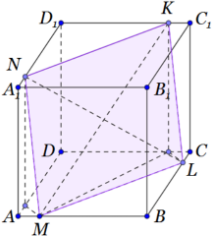
В треугольнике MNKL вычислим стороны и диагональ MK. Если все стороны будут равны и один из углов будет 90°, то MNKL – квадрат.
$NK^2=KD_1^2+ND_1^2=5^2+5^2=50 \\ NK=\sqrt{50}=5\sqrt{2}$
Аналогично $ML=5\sqrt{2}$.
$NM^2=AA_1^2+2AM^2=48+2=50 \\ NM=5\sqrt{2}$
Аналогично $ML=5\sqrt{2}$.
$MK^2=CC_1^2+(MB-KC_1)^2+BC^2=48+16+36=100$
Рассмотрим треугольники MKL и MKN. Они будут прямоугольными:
$MK^2=ML^2+LK^2=100 \\ MK^2=MN^2+NK^2=100$
Значит, MNKL – квадрат.
2) Для того, чтобы найти площадь, нам нужно построить сечение.
Построим след прямой NK на плоскости ABB1 и BCC1.
$NK\cap A_1B_1=P \\ NK\cap B_1C_1=Q$
Точки P и M лежат в плоскости ABB1, соединим эти точки. Причем $PM\cap AA_1=E$.
Точки Q и L лежат в плоскости BCC1, соединим эти точки. Причем $QL\cap CC_1=F$.
Соединяем точки, лежащие в одной грани и получаем сечение MLFKNE.
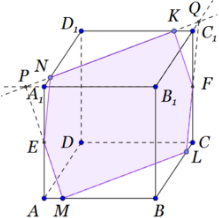
2) Рассмотрим треугольник A1PN.
Значит, $PA_1=1$.
Рассмотрим треугольники PA1E и MAE:
Следовательно, $\angle A_1PE=EMA$
Треугольники PA1E и MAE равны по 2м углам и стороне между ними (равенство всех углов в треугольнике доказали, $A_1P=AM=1$).
Таким образом, $AE=EA_1=3$. Точка Е – середина ребра АА1.
Аналогично доказывается, что точка F – середина ребра СС1.
3) Рассмотрим прямоугольник AEFC. $EF=AC=6\sqrt{2}$.
4) Сечение MLFKNE состоит из двух равнобедренных трапеций ENKF и EMLF.
Причем прямая MN перпендикулярна основаниям NK и ML по доказанному в пункте а).
Тогда:
$S_{MLFKNE}=S_{ENKF}+S_{EMLF}=2\cdot\displaystyle\frac{EF+ML}{2}\cdot\frac{MN}{2}=2\cdot\frac{5\sqrt{2}+6\sqrt{2}}{2}\cdot\frac{5\sqrt{2}}{2}=11\sqrt{2}\cdot\frac{5\sqrt{2}}{2}=55$
В правильной четырёхугольной пирамиде SABCD с основанием ABCD проведено сечение через середины рёбер AB и BC и вершину S. Найдите площадь этого сечения, если все рёбра пирамиды равны 8.
Изобразим указанное в условии сечение ― треугольник SKM; KM = $\displaystyle\frac{1}{2}$ ∙ AC = $\displaystyle\frac{1}{2}$ ∙ 8√2 = 4√2.
Проведем в треугольнике SKM высоту SР. Точка Р ― середина КМ.
Значит, KP = $\displaystyle\frac{1}{2}$ ∙ KM = 2√2.
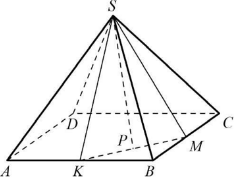
Из треугольника SKА находим SK = $\sqrt{SA^2-AK^2}=\sqrt{64-16}$ = √48.
Из треугольника SPK находим SP = $\sqrt{SK^2-KP^2}=\sqrt{48-8}$ = 2√10.
Тогда: SSKM = $\displaystyle\frac{1}{2}$KM ∙ SP = $\displaystyle\frac{1}{2}$ ∙ 4√2 ∙ 2√10 = 8√5.
В правильной треугольной призме ABCA1B1C1 стороны основания равны 6, боковые рёбра равны 4. Изобразите сечение, проходящее через вершины A, B и середину ребра A1С1. Найдите его площадь.
Обозначим через M и N середины рёбер А1С1 и B1С1 соответственно. По теореме о средней линии треугольника MN || A1B1 || AB, так что прямые MN и AB лежат в одной плоскости. Сечение, про которое спрашивается в условии, — это сечение призмы этой плоскостью. Оно представляет собой равнобокую трапецию AMNB.
Основания трапеции AB = 6, MN = 3; по теореме Пифагора найдем боковую сторону: $AM=\sqrt{AA_1^2+A_1M^2}=\sqrt{16+9}=5$.
Проведём в трапеции высоту MH. Отрезок АН равен полуразности оснований трапеции: AH = $\displaystyle\frac{AB-MN}{2}$ = $\displaystyle\frac{3}{2}$.
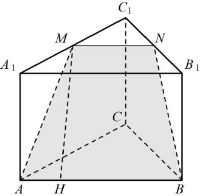
Следовательно, высота трапеции: MH = $\sqrt{5^2-\left({\small\displaystyle\frac{3}{2}}\right)^2}$ = $\displaystyle\frac{\sqrt{91}}{2}$.
Зная ее, находим площадь трапеции: SAMNB = $\displaystyle\frac{MN+AB}{2}\cdot MH=\frac{9}{2}\cdot\frac{\sqrt{91}}{2}=\frac{9}{4}\sqrt{91}$.

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

«Выбери тест, предмет и нажми кнопку «Начать решать»

После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию

Решай задания и записывай ответы. После 1-ой попытки ты сможешь посмотреть решение

Сбоку ты можешь посмотреть статистику и прогресс по предмету

Нажми, чтобы начать решать вариант. Как только ты перейдешь на страницу, запустится счетчик времени, поэтому подготовь заранее все, что может тебе понадобиться

Отмечай те статьи, что прочитал, чтобы было удобнее ориентироваться в оглавлении

Ты прошел обучение! Теперь ты знаешь как пользоваться сайтом и можешь переходить к решению заданий