1) Искомое расстояние — перпендикуляр, опущенный из точки А на прямую ВС₁. По сути, перпендикуляр — это высота в треугольнике АВС₁, опущенная из вершины А на сторону ВС₁. Будем её искать.

2) В квадрате ВСС₁В₁ диагональ ВС₁ равна √2.

В прямоугольном треугольнике АСD находим AC по теореме Пифагора:

AC² = AD² – DC².

$AC=\sqrt{2^2-1^2}=\sqrt{3}$.

Из прямоугольного треугольника АСС₁ имеем $AC_1=\sqrt{\left(\sqrt{3}\right)^2+1^2}=2$ по теореме Пифагора.

3) В треугольнике АВС₁, используя теорему косинусов, получаем:

B AB² = AC₁² + BC₁² – 2 ∙ AC₁ ∙ BC₁ ∙ cosAC₁B;

1 = 4 + 2 – 2 ∙ 2 ∙ √2 ∙ cosAC₁B;

cosAC₁B = $\displaystyle\frac{5}{4\sqrt{2}}$.

Найдем высоту АН:

$\sin AC_1B=\displaystyle\frac{AH}{AC_1}=\frac{AH}{2}$;

AH = sinAC₁B ∙ 2.

Найдем sinAC₁B через основное тригонометрическое тождество:

sin²AC₁B = 1 – cos²AC₁B = $1-\displaystyle\frac{25}{32}=\frac{7}{32}=\frac{14}{64}$;

sinAC₁B = $\displaystyle\frac{\sqrt{14}}{8}$.

Тогда АН равно:

AH = $2\cdot\displaystyle\frac{\sqrt{14}}{8}=\frac{\sqrt{14}}{4}$.

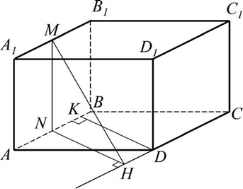
1)Дополнительное построение: проведем MN параллельно АА₁. Так как АА₁ — перпендикуляр к плоскости основания параллелепипеда, то MN также является перпендикуляром к плоскости основания.

Отрезок NH, проведенный перпендикулярно прямой CD является проекцией наклонной MH на плоскость АВС.

$\left.\begin{gathered}MN\perp ABC\rightarrow MN\perp CD \\ NH\perp CD \\ MH\ -\ наклонная\end{gathered}\right\}\rightarrow MH\perp CD\ {(по\ теореме\ о\ трёх\atop перпендикулярах)}$

MH — искомое расстояние.

2) Посмотрим, что дано в условии:

S_бок = $4S_{AA_1B_1B}$ = 4AB · AA₁ = 32AA₁ = 128;

AA₁ = 4.

3) MN = AA₁ = 4, а KD — высота ромба, длина которой вычисляется из треугольника AKD, в котором катет KD лежит напротив угла в 30º, значит, NH = KD = 4.

По теореме Пифагора из треугольника MNH получим:

МН² = MN² + NH²

МН² = 16 + 16 = 32

МН = 4√2.

1) Искомое расстояние d есть длина перпендикуляра А₁М, опущенного на прямую ВС. Поскольку A₁D₁ || BC, это расстояние равно также высоте ВН трапеции А₁ВСD₁.

2) Боковая сторона данной трапеции:

AA₁² + AB² = A₁B²;

4 + 4 = 8 = A₁B²;

A₁B = 2√2.

Нарисуем эту трапецию отдельно:

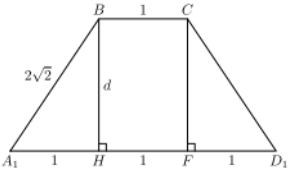
Легко находим: A₁H = $\displaystyle\frac{A_1D_1-BC}{2}$ = 1.

Тогда найдем d по теореме Пифагора:

d² = A₁B² – A₁H² = 8 – 1 = 7

d = √7.

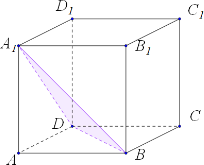
Первый способ

1) Дополнительной построение: пусть О — середина отрезка BD.

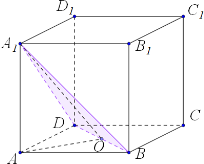
АО — медиана в равнобедренном треугольнике ABD. Значит, по свойству равнобедренного треугольника, АО — высота.

$\left.\begin{gathered}AO\perp BD \\ BD\perp AA_1 \\ AO\cap AA_1=A\end{gathered}\right\}\rightarrow BD\perp AA_1O\ {(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)}$

Значит, BD перпендикулярно любой прямой, лежащей в этой плоскости.

Дополнительное построение. АН перпендикулярно А₁О.

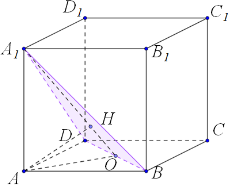
$\left.\begin{gathered}AH\perp A_1O \\ BD\perp AH \\ AO\cap BD=O\end{gathered}\right\}\rightarrow AH\perp A_1BD\ {(по\ признаку\ перпендикулярности\atop прямой\ и\ плоскости)}$

Следовательно, искомым перпендикуляром, опущенным из точки А на плоскость ВDА₁, является высота АН прямоугольного треугольника АОА₁, в котором:

АА₁ = 1, АО = $\displaystyle\frac{\sqrt{2}}{2}$ (как половина диагонали грани куба).

Найдем ОА₁ по теореме Пифагора:

OA₁² = AO² + AA₁² = $1+\displaystyle\frac{2}{4}=\frac{6}{4}$

OA₁ = $\displaystyle\frac{\sqrt{6}}{2}$.

Высота в прямоугольном треугольнике находится по формуле:

$h=\displaystyle\frac{ab}{c}=\frac{1\cdot\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}}{2}}=\frac{\sqrt{2}}{\sqrt{6}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.

Второй способ

Воспользуемся методом двойного выражения объемов.

$V_{AA_1BD}=\displaystyle\frac{1}{3}\cdot S_{ABD}\cdot AA_1=\frac{1}{3}S_{A_1BD}\cdot h$, где h — искомый перпендикуляр.

Тогда:

$h=\displaystyle\frac{S_{ABD}\cdot AA_1}{S_{A_1BD}}=\frac{\frac{1}{2}\cdot AB\cdot AD\cdot AA_1}{BD^2\cdot\frac{\sqrt{3}}{4}}=\frac{4}{2\cdot2\cdot\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.

Первый способ

Воспользуемся методом двойного выражения объемов:

$V_{MBC_1D}=\displaystyle\frac{1}{3}\cdot S_{MC_1D}\cdot BC=\frac{1}{3}\cdot S_{DC_1B}\cdot h$, где h — искомое расстояние.

$h=\displaystyle\frac{S_{MC_1D}\cdot BC}{S_{DC_1B}}=\frac{\frac{1}{2}\cdot MD\cdot C_1D_1\cdot BC}{\frac{BD^2\sqrt{3}}{4}}=\frac{\frac{1}{2}\cdot3\cdot6\cdot6}{\frac{\left(6\sqrt{2}\right)^2\sqrt{3}}{4}}=\frac{4\cdot3\cdot6\cdot6}{2\cdot6\cdot6\cdot2\cdot\sqrt{3}}=\sqrt{3}$.

Второй способ

Пусть искомое расстояние от точки М до плоскости ВС₁D равно d. Тогда расстояние от точки D₁ до этой плоскости равно 2d. Отрезок D₁C делится плоскостью ВС₁D пополам, поэтому расстояние от точки С до данной плоскости также равно 2d.

С другой стороны, расстояние от точки С до плоскости ВС₁D есть высота СН треугольной пирамиды ВС₁DC. Основанием этой пирамиды служит равносторонний треугольник ВС₁D со стороной 6√2. Боковые рёбра пирамиды равны 6. Стало быть, данная пирамида является правильной, и точка Н — центр треугольника ВС₁D.

Отрезок С₁Н есть радиус окружности, описанной вокруг треугольника ВС₁D. Имеем:

$C_1H=\displaystyle\frac{6\sqrt{2}}{\sqrt{3}}=2\sqrt{6}$.

Тогда $CH=\sqrt{CC_1^2-C_1H^2}=\sqrt{6^2-\left(2\sqrt{6}\right)^2}=2\sqrt{3}$. Следовательно, $d=\displaystyle\frac{CH}{2}=\sqrt{3}$.

Первый способ

Дополнительное построение: ST – высота пирамиды SABCD

Воспользуемся методом двойного выражения объемов:

$V_{DBCS}=\displaystyle\frac{1}{3}\cdot S_{BCD}\cdot ST=\frac{1}{3}\cdot S_{BCS}\cdot h$, где h — искомый перпендикуляр.

$h=\displaystyle\frac{S_{BCD}\cdot ST}{S_{BCS}}=\frac{\left(\frac{1}{2}\cdot CD\cdot BC\cdot ST\right)}{S_{BCS}} \\[15pt] S_{BCS}=\displaystyle\frac{1}{2}\cdot h_{BC}\cdot BC \\[15pt] h_{BC}=\sqrt{ST^2+MT^2}=\sqrt{1+1}=\sqrt{2} \\[10pt] S_{BCS}=\displaystyle\frac{1}{2}\cdot h_{BC}\cdot BC=\frac{1}{2}\cdot\sqrt{2}\cdot2=\sqrt{2} \\[15pt] h=\displaystyle\frac{\left(\frac{1}{2}\cdot CD\cdot BC\cdot ST\right)}{S_{BCS}}=\frac{\frac{1}{2}\cdot2\cdot2\cdot1}{\sqrt{2}}=\sqrt{2}$

Второй способ

Пусть SТ — высота пирамиды. Точка Т является серединой отрезка DВ. Тогда искомое расстояние d от точки D до плоскости ВСS равно удвоенному расстоянию от точки Т до этой плоскости по теореме Фалеса.

Расстояние от точки Т до плоскости ВСS равно высоте ТН треугольника SТМ (точка М — середина ВС). Действительно, ТН перпендикулярна также прямой ВС ( BC ⊥ TM, BC ⊥ SM ⇒ BC ⊥ STM ⇒ BC ⊥ TH), и потому ТН — перпендикуляр к плоскости ВСS. Из треугольника SТМ легко находим: ТН = $\displaystyle\frac{\sqrt{2}}{2}$. Тогда d = 2 · TH = √2.

а) SABC — правильная пирамида, значит, О — центр вписанной и описанной окружности основания АВС. Таким образом, точки В, О и N лежат на одной прямой.

Пусть прямая NP пересекает прямую BS в точке К.

Рассмотрим треугольник SNB. Он равнобедренный, так как SN и BN — медианы в равных равносторонних треугольниках.

Найдем величину ON и ОР.

$ON=\displaystyle\frac{1}{3}BN=\frac{1}{3}\cdot\frac{AB\sqrt{3}}{2}=\frac{1}{3}\cdot\frac{4\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}$;

$OB=\displaystyle\frac{2}{3}BN=\frac{4\sqrt{3}}{3}$.

Найдем SO по теореме Пифагора из треугольника BSN:

$SO^2=BS^2-BO^2=SO^2=16-16\cdot\displaystyle\frac{3}{9}=16\cdot\frac{6}{9}$;

$SO=4\cdot\displaystyle\frac{\sqrt{6}}{3}$;

$OP=\displaystyle\frac{1}{4}OS=\frac{1}{4}\cdot4\cdot\frac{\sqrt{6}}{3}=\frac{\sqrt{6}}{3}$.

Найдём PN по теореме Пифагора:

$PN^2=ON^2+OP^2=\displaystyle\frac{12}{9}+\frac{6}{9}=\frac{18}{9}=2$;

$PN=\sqrt{2}$.

Тогда:

$\cos ONP=\displaystyle\frac{ON}{PN}=\frac{2\sqrt{3}}{3}:\sqrt{2}=\frac{\sqrt{6}}{3}; \\[15pt] BS^2=BN^2+SN^2-2\cdot BN\cdot SN\cdot\cos SNB; \\[12pt] 16=12+12-2\cdot2\sqrt{3}\cdot2\sqrt{3}\cdot\cos SNB; \\[12pt] -8=-24\cos SNB; \\[10pt] \cos SNB=\displaystyle\frac{1}{3}.$

Найдем косинус угла, который в два раза меньше, чем угол SNB:

$\cos SNB=2\cos^2 \displaystyle\frac{SNB}{2}-1; \\[15pt] \displaystyle\frac{1}{3}=2\cdot\cos^2 \frac{SNB}{2}-1; \\[15pt] \cos^2 \displaystyle\frac{SNB}{2}=\frac{2}{3}; \\[15pt] \cos\displaystyle\frac{SNB}{2}=\sqrt{{\small\frac{2}{3}}}=\frac{\sqrt{6}}{3}=\cos ONP.$

Значит, угол ОNP является половиной угла SNB. Следовательно, NK — биссектриса в равнобедренном треугольнике, проведенная на основание, а по свойству равнобедренного треугольника эта биссектриса является высотой. Значит, что прямая NP перпендикулярна прямой BS.

б) Так как NK является и высотой, и медианой в равнобедренном треугольнике SNB, то расстояние от точки B до прямой PN равно $BK=\displaystyle\frac{1}{2}BS=2$.

а) Прямая MN параллельна плоскости ABC, поэтому сечение пересекает плоскость ABC по прямой PQ, параллельной MN. Рассмотрим плоскость SCE. Пусть K — точка пересечения этой плоскости и прямой MN, L — точка пересечения этой плоскости и прямой PQ, O — центр основания пирамиды.

Плоскости SCE и MNQ перпендикулярны плоскости ABC, поэтому прямая KL перпендикулярна плоскости ABC, а значит, параллельна прямой SO.

Поскольку MN — средняя линия треугольника ASB, точка K является серединой ES. Следовательно, L — середина EO. Медиана CE треугольника ABC делится точкой O в отношении 2 : 1. Значит, CL : LE = 5 : 1.

б) Прямая CE перпендикулярна KL и PQ, поэтому прямая CE перпендикулярна плоскости MNQ. Прямые AB и PQ параллельны, значит, расстояние от вершины A до плоскости сечения равно расстоянию от точки E до плоскости сечения, то есть $EL=\displaystyle\frac{CE}{6}=5\sqrt{3}$.

а) 1) Дополнительное построение: пусть М — середина AS, K — середина АС, Т — середина АВ. Если мы соединим эти три точки, то получим плоскость.

Отрезки МК, КТ, МТ для треугольников ASC, SCB, ASB будут являться средними линиями.

2) Также давайте посмотрим на плоскости МКТ и SCB. Они параллельные, причем этому способствует признак параллельных плоскостей (две пересекающиеся прямые МК и МТ, принадлежащие плоскости МКТ, соответственно параллельны пересекающимся прямым SC и SB, принадлежащим плоскости SCB).

3) Отпустим перпендикуляр из точки А на плоскость МКТ и назовем его h₁. Тогда продолжение этого перпендикуляра до плоскости SBC будет являться высотой, так как плоскости МКТ и SBC параллельны. Назовем этот перпендикуляр h₂.

4) У нас есть два перпендикуляра, которые мы не можем изобразить. Давайте найдем отношение объемов пирамиды МАТК и SABC.

$V_{MATK}=\displaystyle\frac{1}{3}\cdot MA\cdot S_{ATK}$

$V_{SABC}=\displaystyle\frac{1}{3}\cdot SA\cdot S_{ABC}$

По условию $\displaystyle\frac{MA}{SA}=\frac{1}{2}$, так как М — середина.

Треугольник АТК подобен треугольнику АВС по двум соответствующим сторонам и углу между ними, значит площади этих треугольников относятся как квадрат коэффициента подобия, то есть

$\displaystyle\left(\frac{1}{2}\right)^2=\frac{1}{4}$

Найдем отношение объемов:

$\displaystyle\frac{V_{MATK}}{V_{SABC}}=\frac{\frac{1}{3}\cdot MA\cdot S_{ATK}}{\frac{1}{3}\cdot SA\cdot S_{ABC}}=\frac{MA}{SA}\cdot\frac{S_{ATK}}{S_{ABC}}=\frac{1}{2}\cdot\frac{1}{4}=\frac{1}{8}$.

Используем метод двойного выражения объемов, тогда:

$V_{MATK}=\displaystyle\frac{1}{3}\cdot h_1\cdot S_{MTK}$

$V_{SABC}=\displaystyle\frac{1}{3}\cdot h_2\cdot S_{SBC}$

Треугольники МТК и SBC подобны по трем сторонам, следовательно, их площади относятся, как $\displaystyle\frac{1}{4}$.

Тогда запишем отношение объемов:

$\displaystyle\frac{V_{MATK}}{V_{SABC}}=\frac{\frac{1}{3}\cdot h_1\cdot S_{MTK}}{\frac{1}{3}\cdot h_2\cdot S_{SBC}}=\frac{h_1}{h_2}\cdot\frac{S_{MTK}}{S_{SBC}}=\frac{h_1}{h_2}\cdot\frac{1}{4}=\frac{1}{8}$

Откуда получим, что $\displaystyle\frac{h_1}{h_2}=\frac{1}{2}$. Что и требовалось доказать.

б) 1) Мы знаем, что расстояние от точки А до плоскости МКТ меньше в два раза, чем до плоскости SBC.

$h_1=\displaystyle\frac{h_2}{2}$

Найдем расстояние от точки А до плоскости SBC, а потом просто поделить пополам.

2) h₁ и h₂ расстояния — это высоты в пирамидах.

$V_{SABC}=\displaystyle\frac{1}{3}\cdot SA\cdot S_{ABC}=\frac{1}{3}\cdot h_2\cdot S_{SBC}$

Треугольник АВС — равнобедренный, найдем высоту AD по теореме Пифагора:

$AD^2=AC^2-CD^2=20 \\[9pt] AD=2\sqrt{5}$

Тогда площадь треугольника АВС равна:

$S=\displaystyle\frac{1}{2}\cdot2\sqrt{5}\cdot2\sqrt{5}=10$

3) SC будет равно SB, это можно доказать легко с помощью теоремы Пифагора.

Найдем один из этих отрезков по этой же теореме.

$SC^2=5+25=30 \\[9pt] SC=\sqrt{30}$

Аналогично треугольнику АВС найдем площадь в треугольнике SBC.

$SD^2=30-5=25 \\[9pt] SD=5$

Найдем площадь треугольника SBC:

$S=\displaystyle\frac{1}{2}\cdot5\cdot2\sqrt{5}=5\sqrt{5}$

4) Подставим всё найденное в формулу:

$\displaystyle\frac{1}{3}\cdot SA\cdot S_{ABC}=\frac{1}{3}\cdot h_2\cdot S_{SBC} \\[15pt] SA\cdot S_{ABC}=h_2\cdot S_{SBC} \\[10pt] \sqrt{5}\cdot10=h_2\cdot5\sqrt{5}$

Откуда $h_2=2$.

Тогда $h_1=\displaystyle\frac{h_2}{2}=\frac{2}{2}=1$.