


0
из 6Решил заданий
0
из 6Не решил заданий
6
из 6Осталось заданий
Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие "буква" - "цифра" должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Неравенства с модулем
6 заданийРешите неравенство
$3|x+1| \geq x+5$.
Данное неравенство равносильно совокупности двух систем:
(1) $\begin{cases} x+1 < 0, \\ -3x-3 \geq x +5 \end{cases}$ ⇔ $\begin{cases} x < -1, \\ -4x\geq 8 \end{cases}$ ⇔ $\begin{cases} x < -1, \\ x\leq -2 \end{cases}$ ⇒ x ≤ −2 или x ϵ (−∞; −2].
(2) $\begin{cases} x+1 \geq 0, \\ 3x+3\geq x+ 5 \end{cases}$ ⇔ $\begin{cases} x \geq -1, \\ 2x \geq 2 \end{cases}$ ⇔ $\begin{cases} x \geq -1, \\ x \geq 1 \end{cases}$ ⇒ x ≥ 1 или x [1; +∞).
Объединяя решения двух систем, получим: (−∞; −2] ⋃ [1; +∞).
Решите неравенство
$25x^2 - 4|8-5x| < 80x - 64$
Преобразуем неравенство:
25x2 – 80x + 64 – 4│8 – 5x│ < 0;
(5x − 8)2 − 4│5x − 8│ < 0.
Сделаем замену y = │5x − 8│. Получаем неравенство второй степени y2 – 4y < 0, откуда 0 < y < 4.
Обратная замена дает: 0 < │5x − 8│ < 4, откуда 0,8 < x < 2,4 и $5x - 8 \neq 0 \rightarrow x\neq 1,6$
Решите неравенство
$|x+2| - x|x|\leq 0$
Решим неравенство │x + 2│ − x·│x│ ≤ 0. При любом x ≤ 0 неравенство │x + 2│ − x·│x │ ≤ 0 не выполняется.
При x > 0 неравенство равносильно неравенству x + 2 – x2 ≤ 0 ⇔x2 − x – 2 ≥ 0, решением, которого с учётом условия x > 0 является луч x ≥ 2.
Решить неравенство │2x + 5│ ≥ 7.
Это неравенство равносильно совокупности двух систем:
(1) $\begin{cases} 2x+5 < 0, \\ -2x - 5\geq 7 \end{cases}$ ⇔ $\begin{cases} 2x < -5, \\ -2x \geq 12 \end{cases}$ ⇔ $\begin{cases} x < -2,5, \\ x \leq -6 \end{cases}$ ⇒ x ≤ −6, т. е. x ϵ (−∞; −6].
(2) $\begin{cases} 2x+5 \geq 0, \\ 2x + 5\geq 7 \end{cases}$ ⇔ $\begin{cases} 2x \geq -5, \\ 2x \geq 2 \end{cases}$ ⇔ $\begin{cases} x \geq -2,5, \\ x \geq 1 \end{cases}$ ⇒ x ≥ 1, т. е. x ϵ [1; +∞).
Объединяя решения двух систем, получаем ответ.
Решить неравенство │x2 + 2x − 4│ > 4.
Левая часть неравенства неотрицательна, а правая положительна. Возведем обе части неравенства в квадрат, получим:
(x2 + 2x − 4)2 > 42 ⇔ (x2 + 2x − 4)2 – 42 > 0 ⇔ (x2 + 2x – 4 − 4) · (x2 + 2x – 4 + 4) > 0 ⇔ (x2 + 2x − 8) · (x2 + 2x) > 0 ⇔
⇔ x · (x + 4) · (x − 2) · (x +2) > 0.

x ϵ (−∞; −4) ⋃ (−2; 0) ⋃ (2; +∞).
Решить неравенство x2 + 3·│x − 1│ − 7 > 0.
I способ
Преобразуем неравенство: 3 │x − 1│ > 7 – x2.
Рассмотрим два случая. 1-й случай, если 7 – x2 < 0:
x2 – 7 > 0 ⇔ (x + √7) · (x − √7) > 0 ⇒ x ϵ (−∞; −√7) ⋃ (√7; +∞), тогда неравенство выполняется.
2-й случай, если 7 – x2 ≥ 0, тогда неравенство равносильно системе:
$\begin{cases} 7-x^2 \geq 0, \\ (3(x-1))^2 \geq (7-x^2)^2 \end{cases}$ ⇔ $\begin{cases} x^2 -7 \leq 0, \\ (3(x-1))^2 - (7-x^2)^2 \geq 0\end{cases}$ ⇔ $\begin{cases}(x+\sqrt{7})(x-\sqrt{7}) \leq 0, \\ (3x-3+7-x^2)(3x-3-7+x^2) \geq 0\end{cases}$ ⇔
⇔ $\begin{cases}(x+\sqrt{7})(x-\sqrt{7}) \leq 0, \\ (x^2-3x -4)(x^2 +3x -10) \leq 0\end{cases}$
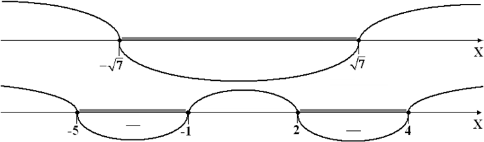
x ϵ [−√7; −1] ⋃ [2; √7].
Объединяя результаты решения в каждом из двух случаев, получаем:
x ϵ (−∞; −√7) ⋃ [−√7; −1] ⋃ [2; √7] ⋃ (√7; +∞), x ϵ (−∞; −1] ⋃ [2; +∞).
II способ
Данное неравенство равносильно совокупности двух систем:
(1) $\begin{cases} x-1 < 0, \\ x^2 -3x + 3 - 7 > 0 \end{cases}$ ⇔ $\begin{cases} x < 1, \\ x^2 -3x + -4 > 0 \end{cases}$ ⇔ $\begin{cases} x < 1, \\ (x+1)(x-4) > 0 \end{cases}$
Изобразим решения каждого из неравенств на числовой прямой, получим:
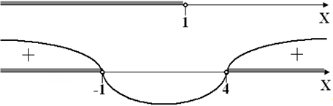
x ϵ (−∞; −1)
(2) $\begin{cases} x-1 \geq 0, \\ x^2 +3x -3-7 > 0, \end{cases}$ ⇔ $\begin{cases} x \geq 1, \\ x^2 +3x -10 > 0, \end{cases}$ ⇔ $\begin{cases} x \geq 1, \\ (x+5)(x-2) > 0, \end{cases}$
Изобразим решения каждого из неравенств на числовой прямой, получим:
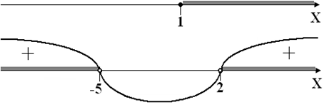
x ϵ (2; +∞).
Объединяя решения 1-й и 2-й систем, получаем: x ϵ (−∞; −1) ⋃ (2; +∞).

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

«Выбери тест, предмет и нажми кнопку «Начать решать»

После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию

Решай задания и записывай ответы. После 1-ой попытки ты сможешь посмотреть решение

Сбоку ты можешь посмотреть статистику и прогресс по предмету

Нажми, чтобы начать решать вариант. Как только ты перейдешь на страницу, запустится счетчик времени, поэтому подготовь заранее все, что может тебе понадобиться

Отмечай те статьи, что прочитал, чтобы было удобнее ориентироваться в оглавлении

Ты прошел обучение! Теперь ты знаешь как пользоваться сайтом и можешь переходить к решению заданий