


0
из 11Решил заданий
0
из 11Не решил заданий
11
из 11Осталось заданий
Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие "буква" - "цифра" должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Алгебраические методы решения
11 заданийПри каких значениях параметра а сумма квадратов корней уравнения 2log4(2x2 – x + 2a – 4a2) + log0,5(x2 + ax – 2a2) = 0 больше 1?
На основании свойств логарифмов исходное уравнение равносильно уравнению log2(2x2 – x + 2a – 4a2) = log2(x2 + ax – 2a2), , которое, в свою очередь, равносильно системе: $\begin{cases} x^2 - (a+1)x + 2a (1-a) = 0 \\ (x + 2a)(x-a) > 0\end{cases}$.
Уравнение записанной системы имеет корни x1 = 1 − a и x2 = 2a.
Подставляя поочерёдно полученные значения х в неравенство системы, получим систему: $\begin{cases} (a+1)(2a-1) < 0 \\ 4a^2 > 0 \end{cases}$, из которой находим, что a ϵ (−1; 0) ⋃ $(0; \displaystyle \frac{1}{2})$.
Учитывая теперь, что x12 + x22 = 5a2 – 2a + 1, из неравенства 5a2 – 2a + 1 > 1 получаем значения a ϵ (−∞; 0) ⋃ $(\displaystyle \frac{2}{5}; +\infty)$.
При каких значениях параметра а сумма loga $(\displaystyle \frac{3+2x^2}{1+x^2})$ и loga $(\displaystyle \frac{5+4x^2}{1+x^2})$ больше единицы ри всех х?
Рассмотрим сумму логарифмов:
S = loga $(\displaystyle \frac{3+2x^2}{1+x^2})$ + loga $(\displaystyle \frac{5+4x^2}{1+x^2})$ = loga $(2 + \displaystyle \frac{1}{1+x^2})$ + loga $(4 + \displaystyle \frac{1}{1+x^2})$
Эта сумма имеет смысл при любых х. Заменим t = $\displaystyle \frac{1}{1+x^2}$, тогда очевидно, что
0 < t ≤ 1.
Составим неравенство: loga(2 + t) + loga(4 + t) > 1 и найдём значения параметра а, при которых неравенство выполняется при всех t ϵ (0; 1].
Если a > 1, то логарифмическая функция возрастает. Запишем равносильное неравенство (2 + t)(4 + t) > a или t2 + 6t + 8 – a > 0.
Абсцисса вершины параболы f (t) = t2 + 6t + 8 – a равна t0 = −3, ветви направлены вверх, следовательно, на интервале (0; 1] функция f (t) монотонно возрастает.
Неравенство f (t) > 0 выполняется тогда и только тогда, когда f (0) ≥ 0, откуда 1 < a ≤ 8.
При 0 < a < 1 исходное неравенство равносильно следующему: f (t) = t2 + 6t + 8 – a < 0.
Аналогично первому случаю, функция f (t) монотонно возрастает на (0; 1], поэтому необходимо и достаточно выполнения условия f (1) < 0, т. е. 1 + 6 + 8 – a < 0, a > 15. Полученный ответ не имеет пересечений с условием 0 < a < 1.
Тогда получаем искомые значения a ϵ (1; 8].
Найдите все значения a, при каждом из которых неравенство
$\bigg| \displaystyle \frac{x^2 + ax + 1 }{x^2 + x + 1}\bigg| < 3$
выполняется при всех х.
$\bigg| \displaystyle \frac{x^2 + ax + 1 }{x^2 + x + 1}\bigg| < 3 \leftrightarrow -3 < \displaystyle \frac{x^2 + ax + 1 }{x^2 + x + 1} < 3 \leftrightarrow \\ \begin{cases} \displaystyle \frac{x^2 + ax + 1 }{x^2 + x + 1} < 3 \\ \displaystyle \frac{x^2 + ax + 1 }{x^2 + x + 1} > -3 \end{cases} \leftrightarrow \begin{cases} \displaystyle \frac{x^2 + ax + 1 - 3 (x^2 + x+ 1)}{x^2 + x+1} < 0 \\ \displaystyle \frac{x^2 + ax + 1 + 3 (x^2 + x+ 1)}{x^2 + x+1} > 0 \end{cases} \leftrightarrow \begin{cases} \displaystyle \frac{x^2 + ax + 1 - 3x^2 -3x- 3}{x^2 + x+1} < 0 \\ \displaystyle \frac{x^2 + ax + 1 + 3x^2 +3x+3}{x^2 + x+1} > 0 \end{cases} \leftrightarrow \\ \leftrightarrow \begin{cases} \displaystyle \frac{-2x^2 + ax - 3x -2}{x^2 + x + 1} < 0 \\ \displaystyle \frac{4x^2 + ax + 3x +4}{x^2 + x + 1} > 0 \end{cases} \leftrightarrow \begin{cases} \displaystyle \frac{2x^2 - ax + 3x +2}{x^2 + x + 1} > 0 \\ \displaystyle \frac{4x^2 + ax + 3x +4}{x^2 + x + 1} > 0 \end{cases} \leftrightarrow \begin{cases} \displaystyle \frac{2x^2 - (a - 3)x +2}{x^2 + x + 1} > 0 \\ \displaystyle \frac{4x^2 + (a + 3)x + 4}{x^2 + x + 1} > 0 \end{cases}$
Рассмотрим знаменатель данных дробей.
$f(x) = x^2 + x+1$
Ветви направлены вверх.
$D = 1 - 4\cdot 1\cdot 1 = -3 < 0$
Значит, $f(x) = x^2 + x+ 1 > 0$ при любых х. Преобразуем систему.
Решим первое неравенство.
$2x^2 - (a-3)x + 2 > 0 \\ D = (a-3)^2 - 16 = a^2 -6a + 9 -16 = a^2 - 6a - 7$
На данном этапе не знаем знак дискриминанта.
$D = a^2 - 6a - 7< 0 \rightarrow (a-7)(a+1) < 0 \rightarrow a \in (-1; 7)$ - знак неравенства выполняется при всех значениях х.
$D = a^2 -6a - 7 \geq \rightarrow (a - 7)(a+1) \geq 0 \rightarrow a \in (-\infty; -1] \cup [7; +\infty)$- решаем неравенство:
$2(x - \sqrt{a^2 - 6a - 7})(x + \sqrt{a^2 - 6a - 7}) > 0 \\ \rightarrow \begin{cases} x < -\sqrt{a^2 - 6a -7} \\ x > \sqrt{a^2 - 6a - 7}\end{cases}$
Решим второе неравенство.
$4x^2 + (a+3)x + 4 > 0 \\ D= (a+3)^2 - 64 = a^2 + 6a + 9 -64 = a^2 + 6a - 55 $
На данном этапе не знаем знак дискриминанта.
$D = a^2 +6a - 55 < 0 \rightarrow (a-5)(a+11) < 0 \rightarrow a \in (-11; 5)$ - знак неравенства выполняется при всех значениях х.
$D = a^2 + 6a - 55 \geq 0 \rightarrow (a-5)(a+11) \rightarrow a \in (-\infty; -11] \cup [5; +\infty)$- решаем неравенство:
Необходимо, чтобы неравенство выполнялось при всех х. Тогда получим значения (‒1;5).
Найдите все значения a, при каждом из которых уравнение
$\sqrt{3x - 2} \ln (x -a) = \sqrt{3x -2} \ln (2x + a)$
имеет единственный корень на отрезке [0;1].
$\sqrt{3x - 2} \ln (x -a) = \sqrt{3x -2} \ln (2x + a)$
ОДЗ:
Первый случай:
$\sqrt{3x - 2} = 0 \rightarrow 3x - 2 = 0 \rightarrow x = \displaystyle \frac{2}{3}$
Проверим ОДЗ:
Видим, что этот корень возможен при $-\displaystyle \frac{4}{3} < a < \displaystyle \frac{2}{3}$. Он также попадает в нужный нам промежуток [0;1].
Второй случай:
$\ln(x-a) -\ln (2x + a) = 0 \\ \ln(x - a) = ln (2x + a) \\ x - a = 2x + a \\ x = -2a$
Корень должен лежать на отрезке [0;1].
$0 \leq 0 \leq 1 \\ 0 \leq -2a \leq 1 \\ 0 \leq -a \leq \displaystyle \frac{1}{2} \\ -\displaystyle \frac{1}{2} \leq a \leq 0$
Этот корень также должен удовлетворять ОДЗ всего уравнения, то есть условиям:
$\begin{cases} 3x - 2 \geq 0 \\ x - a > 0 \\ 2x + a > 0\end{cases}$
Подставим $x = -2a$
Значит, второй корень, принадлежащий отрезку [0;1], возможен при $-\displaystyle \frac{1}{2} \leq a \leq -\displaystyle \frac{1}{3}$.
Итак,
$x = -2a , \text{если} -\displaystyle \frac{1}{2} \leq a -\displaystyle \frac{1}{3} \\ x = \displaystyle \frac{2}{3}, \text{если} -\displaystyle \frac{4}{3} < a < \displaystyle \frac{2}{3}$
Запишем по-другому:
Если$-\displaystyle \frac{1}{2} \leq a \leq -\displaystyle \frac{1}{3}$, то уравнение имеет 2 удовлетворяющих условию корня.
Если $-\displaystyle \frac{4}{3} < a < -\displaystyle \frac{1}{2} \text{и} -\displaystyle \frac{1}{3} < a < \displaystyle \frac{2}{3}$, то уравнение имеет только один корень$x = \displaystyle \frac{2}{3}$.
Проверим, при каких значениях a корни совпадают:
$\begin{cases} x = -2a \\ x = \displaystyle \frac{2}{3}\end{cases} \rightarrow -2a = \displaystyle \frac{2}{3} \rightarrow a = -\displaystyle \frac{1}{3}$
Нам необходимо, чтобы уравнение имело единственный корень. Тогда в ответ пойдут промежутки, где существует корень$x = \displaystyle \frac{2}{3}$, то есть $-\displaystyle \frac{4}{3} < a < -\displaystyle \frac{1}{2} \text{и} -\displaystyle \frac{1}{3} < a < \displaystyle \frac{2}{3}$, а также случай, когда корни совпадают.
Найдите все значения параметра a, при которых корни уравнения $(2x + 1)x^2 + (a+3)x + (2-3a)= 0$ меньше ‒1.
Относительно параметра a следует рассмотреть два случая: 2a + 1 = 0 и 2a + 1 ≠ 0.
При 2a + 1 = 0, то есть при a = –$\displaystyle \frac{1}{2}$, получим линейное уравнение 2,5x + 3,5 = 0.
Следовательно, в данном случае x = –1,4 < –1. Таким образом, значение параметра a = –$\displaystyle \frac{1}{2}$удовлетворяет условию поставленной задачи.
Рассмотрим теперь случай 2a + 1 ≠ 0, то есть a ≠ –$\displaystyle \frac{1}{2}$. Приведем данное уравнение к виду x2 + $\displaystyle \frac{(a+3)^2}{(2a + 1)^2}$ + $\displaystyle \frac{(2-3a)}{(2a+1)}$ = 0. Поставленная задача относится к задачам типа 2, поэтому следует проверить условия:
или
Решим каждое неравенство отдельно, а затем найдем пересечение полученных промежутков.
1) $\displaystyle \frac{(a+3)^2}{(2a + 1)^2}$ – 4$\displaystyle \frac{2-3a}{2a+1}$ ≥ 0 ⇔ a2 + 6a + 9 – 4(4a + 2 – 6a2 – 3a) ≥ 0 ⇔ 25a2 + 2a + 1 ≥ 0.
Так как D1 = 1 – 25 = –24 < 0 и 25 > 0, то неравенство 25a2 + 2a + 1 ≥ 0 справедливо для любого действительного числа a. Таким образом, первое неравенство выполняется для любого a ∈ R.
2) $\displaystyle \frac{(2a + 1-a-3+2-3a)}{(2a + 1)} > 0 \Leftrightarrow \displaystyle \frac{(-2a)}{(2a + 1)} > 0 \Leftrightarrow a \in (-\displaystyle \frac{1}{2} ; 0)$
$3) \quad \displaystyle \frac{-(a+3)}{2(2a + 1)} < -1 \Leftrightarrow \displaystyle \frac{-(a+3)}{2(2a+1)} + 1 < 0 \qquad \displaystyle \frac{-a-3+4a+2}{2(2a + 1)} < 0 \Leftrightarrow \displaystyle \frac{3a -1 }{(2a + 1 )} < 0 \Leftrightarrow a \in (-\displaystyle \frac{1}{2}; \displaystyle \frac{1}{3})$
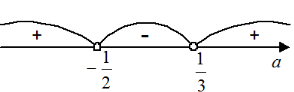
4) Найдем пересечение полученных промежутков: (–∞; + ∞), $(-\displaystyle \frac{1}{2} ; 0)$ и $(-\displaystyle \frac{1}{2} ; \displaystyle \frac{1}{3})$. Таким образом, при a ∈ $(-\displaystyle \frac{1}{2} ; 0)$ исходное уравнение имеет два корня, каждый из которых меньше –1.
Объединяя найденные решения a = – $\displaystyle \frac{1}{2}$ и a ∈ $(-\displaystyle \frac{1}{2} ; 0)$ , окончательно получаем a ∈ $[-\displaystyle \frac{1}{2} ; 0)$.
Получаем: a ∈ $[-\displaystyle \frac{1}{2} ; 0)$
Найдите все значения параметра p, при каждом из которых уравнение $(p+1)x^2 + (p-5)x + 2p = 0$ имеет корни большие 1.
Пусть p + 1 = 0, то есть p = –1. Тогда наше уравнение принимает вид –6x – 2 = 0. Следовательно, оно имеет решение x = –$\displaystyle \frac{1}{3}$ < 1 и параметр p = –1 не удовлетворяет условиям задачи.
Пусть p ≠ –1. Тогда приведем данное уравнение к виду x2 + $\displaystyle \frac{(p-5)}{(p+1)}x$ + $\displaystyle \frac{2p}{(p+1)}$ = 0. При этом параметр p должен удовлетворять системе:
Решим каждое из полученных неравенств в отдельности, а затем найдем пересечение числовых промежутков, являющихся решением этих неравенств.
1) $\displaystyle \frac{(p - 5)^2}{(p+1)^2}$ – 4$\displaystyle \frac{2p}{(p+1)}$ ≥ 0 ⇔ p2 – 10p + 25 – 8p2 – 8p ≥ 0 ⇔ –7p2 – 18p + 25 ≥ 0 ⇔ 7p2 + 18p – 25 ≤ 0.
Так как D1 = 92 + 7 ∙ 25 = 256 = 162, то p1 = $\displaystyle \frac{-9+16}{7}$ = 1, p2 = $\displaystyle \frac{-9-16}{7}$ = –$\displaystyle \frac{25}{7}$ и неравенство 7p2 + 18p – 25 ≤ 0 принимает вид:
7$(p + \displaystyle \frac{25}{7})$ (p – 1) ≤ 0. Отсюда p ∈ $[-\displaystyle \frac{25}{7}; 1]$.
2) $\displaystyle \frac{(p+1+p-5+2p)}{(p+1)}$ > 0 ⇔ $\displaystyle \frac{(4p-4)}{(p+1)}$ > 0 ⇔ $\displaystyle \frac{(p-1)}{(p+1)}$ > 0. Отсюда p ∈ (–∞; –1) ∪ (1; + ∞).
3) $\displaystyle \frac{-(p-5)}{2(p+1)} > 1 \Leftrightarrow \displaystyle \frac{-p+5}{2(p +1 )} -1 \Leftrightarrow \displaystyle \frac{-p+5-2p-2}{2(p+1)} > 0 \Leftrightarrow \displaystyle \frac{p-1}{p+1}$
Отсюда p ∈ (–1; 1).
Таким образом, искомые значения параметра p должны удовлетворять условиям:
p ∈ $[-\displaystyle \frac{25}{7}; 1]$, p ∈ (–∞; –1) ∪ (1; + ∞) и p ∈ (–1; 1). Так как второе и третье условия одновременно не выполняются, то не существует такого значения параметра p, при котором уравнение (p + 1)x2 + (p – 5)x + 2p = 0 имеет корни большие 1.
Найдите все значения а, при каждом из которых уравнение $\displaystyle \frac{4^{-x^2} -a\cdot 2^{1-x^2} +a}{2^{1-x^2} -1} = 3$
имеет хотя бы одно решение.
Поделим числитель и знаменатель дроби на 1 + x2: = 3.
Сделаем замену: z = $\displaystyle \frac{1}{\sqrt{1+x^2}}$.
Тогда $\displaystyle \frac{z^2 -2az + a}{1-2z}$ = 3. Так как 1 + x2 ≥ 1 поэтому 0 < z ≤ 1.
Задачу можно сформулировать так: найдите все значения а, при каждом из которых
уравнение $\displaystyle \frac{z^2 -2az + a}{1-2z}$ = 3 имеет хотя бы одно решение, удовлетворяющее условию 0 < z ≤ 1.
Перейдем к системе:
$\begin{cases} z^2 -2az + a = -6z + 3, \\ z\neq 0,5, \\ 0< z \leq 1; \end{cases}$ ⇔ $\begin{cases} z^2 -2(a-3)z +a - 3 = 0, \\ z\neq 0,5, \\ 0< z \leq 1; \end{cases}$
Заметим, что ни при одном значении а число z = 0,5 не является корнем уравнения.
Рассмотрим функцию f (z) = z2 – 2(a – 3)z + a – 3. Её график — парабола, ветви которой направлены вверх. Следовательно, условие задачи выполнено тогда и только тогда, когда выполняется одно из трёх условий:
Трёхчлен имеет два различных корня, и только больший из них лежит на промежутке (0; 1] (см. рис. 1), то есть $\begin{cases} f(0) < 0, \\ f(1) \geq 0. \end{cases}$
Трёхчлен имеет два различных корня, и только меньший из них лежит на промежутке (0; 1] (см. рис. 2), то есть $\begin{cases} f(0) > 0, \\ f(1) \leq 0. \end{cases}$
Трёхчлен имеет два корня, возможно, совпадающих, и оба лежат на промежутке (0; 1] (см. рис. 3), то есть $\begin{cases} f(0) > 0, \\ f(1) \geq 0, \\ f(z_0) \leq 0 \end{cases}$, где z0 — абсцисса вершины параболы.
Эти условия соответствуют следующим способам расположения графика функции:
Решим систему: $\begin{cases} a - 3 < 0, \\ 1 - a + 3 \geq 0 \end{cases}$ ⇔ $\begin{cases} a < 3, \\4 \leq 4 \end{cases}$ ⇔ a < 3.
Решим систему: $\begin{cases} a - 3 > 0, \\ 1 - a + 3 \leq 0 \end{cases}$ ⇔ $\begin{cases} a > 3, \\4 \geq 4 \end{cases}$ ⇔ a ≥ 4.
Решим систему: ⇔ $\begin{cases} a > 3, \\ a \leq 4 \\ a \geq 4 \end{cases}$ откуда а = 4.
Тогда получаем значения: a < –3; a ≥ –2.
Найти наибольшее целое значение параметра m, при котором корни уравнения (2m – 3)x2 + (4m + 2)x + m2 = 0, при этом x1 и x2 удовлетворяют условию x1 < –1 < x2.
(2m – 3)≠0 так как необходимо, чтобы данное уравнение имело 2 различных корня.
Тогда данный пример относится к типу 1 задач. Приведем уравнение к виду x2 + $\displaystyle \frac{4m + 2}{(2m - 3)}x$ + $\displaystyle \frac{m^2}{(2m - 3)}x$ = 0. Так как x1 < –1 < x2, то рассмотрим такое неравенство f (–1) < 0 или (–1)2 + $\displaystyle \frac{(4m + 2)}{(2m - 3)} (-1)$ + $\displaystyle \frac{m^2}{(2m - 3)}x$ < 0 и получим $\displaystyle \frac{(2m - 3-4m -2-m^2)}{(2m - 3)}$ < 0 или $\displaystyle \frac{(m^2 - 2m - 5)}{(2m - 3)}$ < 0. Разложим квадратный трехчлен m2 – 2m – 5 на множители. Для этого решим уравнение m2 – 2m – 5 = 0. Его корни m1 = 1 – √6 и m2 = 1 + √6. Следовательно, неравенство примет вид < 0.
Для решения этого неравенства воспользуемся методом интервалов:
m ∈ (–∞; 1 – √6) ∪ $(\displaystyle \frac{3}{2}; 1 +\sqrt{6})$.
Найдем наибольшее целое m, принадлежащее указанным промежуткам.
Для этого оценим 1 + √6. Так как 2 < √6 < 3, то 3 < 1 + √6 < 4 и потому 3 ― наибольшее целое m, при котором x1 < –1 < x2.
Найти все значения параметра m, при которых уравнение (m – 1)x2 + (m2 – 2)x + (m – 5) = 0 имеет корни x1 и x2, удовлетворяющие условиям x1 < 0 и x2 > 1.
Из условия задачи следует, что x1 < 0 < x2 и x1 < 1 < x2, значит, m – 1 ≠0.
Приведем данное уравнение к виду x2 + $\displaystyle \frac{(m^2 - 2)}{(m-1)}x$ + $\displaystyle \frac{(m - 5)}{(m -1)}$ = 0 и запишем соответствующие условия, где f (x) = x2 + $\displaystyle \frac{m^2 - 2}{m -1}x$ + $\displaystyle \frac{m - 5}{m -1}$:
или
Решим каждое неравенство системы методом интервалов.
1) $\displaystyle \frac{(m - 5)}{(m -1)}$ < 0, то есть m ∈ (1; 5).
2) $\displaystyle \frac{(m^2 + 2m - 8)}{(m -1)}$ < 0, тогда $\displaystyle \frac{(m + 4)(m-2)}{(m -1 )}$ < 0, то есть m ∈ (–∞; –4) ∪ (1; 2).
Таким образом, исходная система неравенств будет эквивалентна системе: m ∈ (1; 5) ∩ ((–∞; –4) ∪ (1; 2)).
Получаем, что m ∈ (1; 2).
Найдите наименьшее целое значение параметра a, при котором корни уравнения a2x2 + (2a + 3) x + 1 = 0 больше –2.
Рассмотрим два случая: a = 0 и a ≠ 0.
При a = 0 имеем линейное уравнение 3x + 1 = 0. Его решение x = – $\displaystyle \frac{1}{3}$ > –2 удовлетворяет условию задачи.
Рассмотрим теперь случай a ≠ 0. Приведем уравнение к виду x2 + $\displaystyle \frac{(2a+3)}{a^2}x$ + $\displaystyle \frac{1}{a^2}$ = 0. Параметр a должен удовлетворять системе неравенств:
или
Решим каждое полученное неравенство отдельно, а затем найдем пересечение полученных промежутков.
1) $\displaystyle \frac{(2a+3)^2}{a^2}x$ – $\displaystyle \frac{4}{a^2}$ ≥ 0 ⇔ 4a2 + 12a + 9 – 4a2 ≥ 0 ⇔ 12a + 9 ≥ 0 ⇔ a ≥ – $\displaystyle \frac{3}{4}$.
Таким образом, первое неравенство имеет решение a ∈ $[-\displaystyle \frac{3}{4}; +\infty)$
$2) \; \displaystyle \frac{(4a^2 - 4a - 6 +1)}{a^2} > 0 \Leftrightarrow \displaystyle \frac{(4a^2 - 4a - 5)}{a^2} > 0 \Leftrightarrow > 0 \Leftrightarrow a \in (-\infty; \displaystyle \frac{1-\sqrt{6}}{2}) \cup(\displaystyle \frac{1+\sqrt{6}}{2}; + \infty) \\ 3) \; \displaystyle \frac{-(2a + 3)}{2a^2} > -2 \Leftrightarrow \displaystyle \frac{-2a-3}{2a^2} > -2 \Leftrightarrow \displaystyle \frac{-2a-3}{2a^2} + 2 > 0 \Leftrightarrow \displaystyle \frac{-2a-3+4a^2}{2a^2} > 0 \Leftrightarrow >0 \Leftrightarrow a \in (-\infty; \displaystyle \frac{1-\sqrt{13}}{4})$
4) Найдем пересечение полученных интервалов:
a ∈ , a ∈ ∪ и a ∈ ∪ . Получим, что при a ∈ ∪ наше уравнение имеет два корня, каждый из которых больше –2.
Объединяя рассмотренные случаи a = 0 и a ≠ 0, получим множество значений параметра:
a ∈ ∪ {0} ∪ , при которых уравнение имеет два корня, каждый из которых больше –2.
По условию задачи необходимо найти наименьшее целое a. Таким значением параметра является a = 0.
Найдите все значения а, при каждом из которых уравнение $\displaystyle \frac{1-2a\sqrt{1+x^2} +a(1+x^2)}{(1+x^2) -2\sqrt{1+x^2}}$ = 3 имеет хотя бы одно решение.
Поделим числитель и знаменатель дроби на 1 + x2: $\displaystyle \frac{\displaystyle \frac{1}{1+x^2} - \displaystyle \frac{2a}{\sqrt{1+x^2}} + a}{1-\displaystyle \frac{2}{\sqrt{1+x^2}}}$ = 3.
Сделаем замену: z = $\displaystyle \frac{1}{\sqrt{1+x^2}}$.
Тогда $\displaystyle \frac{z^2 -2az + a}{1-2z}$= 3. Так как 1 + x2 ≥ 1 поэтому 0 < z ≤ 1.
Задачу можно сформулировать так: найдите все значения а, при каждом из которых
уравнение $\displaystyle \frac{z^2 -2az + a}{1-2z}$ = 3 имеет хотя бы одно решение, удовлетворяющее условию 0 < z ≤ 1.
Перейдем к системе:
$\begin{cases} z^2 -2az + a = -6z + 3, \\ z \neq 0,5, \\ 0< z \leq 1;\end{cases} \Leftrightarrow \begin{cases} z^2 - 2(a-3) z + a - 3 = 0, \\ z\neq 0,5, \\ 0< x \leq 1\end{cases}$
Заметим, что ни при одном значении а число z = 0,5 не является корнем уравнения.
Рассмотрим функцию f (z) = z2 – 2(a – 3)z + a – 3. Её график — парабола, ветви которой направлены вверх. Следовательно, условие задачи выполнено тогда и только тогда, когда выполняется одно из трёх условий:
Трёхчлен имеет два различных корня, и только больший из них лежит на промежутке (0; 1] (см. рис. 1), то есть
Трёхчлен имеет два различных корня, и только меньший из них лежит на промежутке (0; 1] (см. рис. 2), то есть
Трёхчлен имеет два корня, возможно, совпадающих, и оба лежат на промежутке (0; 1] (см. рис. 3), то есть , где z0 — абсцисса вершины параболы.
Эти условия соответствуют следующим способам расположения графика функции:
Решим систему: $\begin{cases} a - 3 < 0, \\ 1 - a + 3\geq 0 \end{cases} \Leftrightarrow \begin{cases} a < 3, \\ a \leq 4\end{cases}$ ⇔ a < 3.
Решим систему: $\begin{cases} a - 3 > 0, \\ 1 - a + 3\leq 0 \end{cases} \Leftrightarrow \begin{cases} a > 3, \\ a \geq 4\end{cases}$ ⇔ a ≥ 4.
Решим систему: $\begin{cases} a - 3 > 0, \\ 1-2(a-3)+a - 3\geq 0 \\ (a-3)^2 - 2(a-3)^2 + a - 3\leq 0 \end{cases} \Leftrightarrow \begin{cases} a > 3, \\ a \leq 4 \\ a \geq 4 \end{cases}$ откуда а = 4.
Получаем значения: a < 3, a ≥ 4.

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

«Выбери тест, предмет и нажми кнопку «Начать решать»

После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию

Решай задания и записывай ответы. После 1-ой попытки ты сможешь посмотреть решение

Сбоку ты можешь посмотреть статистику и прогресс по предмету

Нажми, чтобы начать решать вариант. Как только ты перейдешь на страницу, запустится счетчик времени, поэтому подготовь заранее все, что может тебе понадобиться

Отмечай те статьи, что прочитал, чтобы было удобнее ориентироваться в оглавлении

Ты прошел обучение! Теперь ты знаешь как пользоваться сайтом и можешь переходить к решению заданий