Область допустимых значений параметра определяется системой $\begin{cases} 1 -a > 0, \\ 1 - a \neq 1 \end{cases}$ Откуда a ϵ (−∞; 0) ⋃ (0; 1).

По свойствам логарифмической функции перепишем уравнение в виде 2 – cosx + sin$\displaystyle \frac{x}{2}$ = (1 − a)².

Заменяя cosx = 1 – 2sin²$\displaystyle \frac{x}{2}$ и полагая t = sin$\displaystyle \frac{x}{2}$, получаем квадратное уравнение: 2t² + t + 2a – a² = 0.

Это уравнение имеет два решения, если D = 8a² – 16a + 1 ≥ 0, откуда с учётом ОДЗ получаем a ϵ (−∞; 0) ⋃ $(0; 1 - \displaystyle \frac{\sqrt{14}}{4}]$.

Найдём теперь, при каких значениях параметра а хотя бы один из корней этого уравнения будет принадлежать отрезку [−1; 1]. Так как ветви параболы f (t) = 2t² + t + 2a – a² направлены вверх, вершина находится в точке t₀ = −$\displaystyle \frac{1}{4}$, то корни располагаются симметрично относительно точки t = −$\displaystyle \frac{1}{4}$. Поэтому, если меньший корень лежит в промежутке [−1; 1], то больший — тем более. Таким образом, достаточно выяснить, при каких значениях параметра а больший корень параболы окажется в промежутке $[-\displaystyle \frac{1}{4}; 1]$. Это будет в том и только в том случае, если f (1) ≥ 0. Вычисляя f (1), получаем неравенство 3 + 2a – a² ≥ 0, которое справедливо при a ϵ [−1; 3]. Пересекая этот промежуток с предыдущим, получаем a ϵ [−1; 0) ⋃ $(0; 1 - \displaystyle \frac{\sqrt{14}}{4}]$.

Мы видим, что это уравнение содержит сложную функцию: tg(cosx), к тому же в это уравнение входит функция x². То есть в одном уравнении две очень разнородные функции. Кажется, обычными методами мы его решить не сможем. Как же подступиться к решению этой задачи? Во-первых, мы отмечаем для себя, что нам нужно найти значение параметра b, при котором уравнение имеет единственное решение. Эти два факта: сложное нерешаемое уравнение и требование единственности решения, являются для нас знаком, что возможно, в этом уравнении присутствует симметрия. Давайте проверим.

Если сделать замену: x ⇒ –x, то x² ⇒ (–x)² = x² и cos(x) ⇒ cos(–x) = cosx ― ничего не меняется. Значит уравнение симметрично относительно замены x ⇒ –x. А это значит, что если число a является корнем уравнения, то число –a тоже является корнем уравнения. Значит, уравнение будет иметь единственное решение, только если x = 0.

Найдем b подставляя x = 0 в исходное уравнение: –btg(cos0) + 1 = 0, откуда b = ctg1.

Но это не является еще полноценным решением. Потому что мы нашли необходимое условие того, чтобы у уравнения было единственное решение. Требуется еще проверить, не возникает ли при таком b дополнительных корней уравнения, таким образом мы докажем достаточность.

Подставим полученное b в исходное уравнение: ctg²1 ∙ x² – ctg1 ∙ tg(cosx) + 1 = 0.

И представим его в следующем виде: $\displaystyle \frac{tg (\cos x)}{tg 1}$ = 1 + $\displaystyle \frac{x^2}{tg^2 1}$.

Тангенс является возрастающей функцией на интервале $\big( -\displaystyle \frac{\pi}{2}; \displaystyle \frac{\pi}{2} \big)$. Косинус, являющийся аргументом тангенса, принимает значение из отрезка [–1; 1], а этот отрезок лежит внутри интервала $\big( -\displaystyle \frac{\pi}{2}; \displaystyle \frac{\pi}{2} \big)$. Следовательно, справедливо неравенство tg(cosx) ≤ tg1, то есть левая часть уравнения: $\displaystyle \frac{tg (\cos x)}{tg 1}$ = 1 + $\displaystyle \frac{x^2}{tg^2 1}$, не превосходит единицу, в тоже время правая часть не меньше 1, и равенство возможно лишь в том случае, когда обе части равны 1, то есть при x = 0.

Итак, мы показали, что условие b = ctg1 является достаточным и необходимым для того, чтобы у исходного уравнения было единственное решение.

Система не меняет своего вида при замене x на –x; значит, если решением системы является пара чисел (x₀, y₀),то пара чисел (–x₀, y₀) тоже являются решением системы. Значит, решение будет единственным, только в случае, если x = 0. Как и в предыдущей задаче найдем для этого необходимое условие (подставим в исходную систему x = 0) $\begin{cases} a - 1 = y \\ y^2 = 1\end{cases}$. Решая систему, получим два возможных варианта:

y = 1, a = 2;

y = –1, a = 0.

Теперь, рассмотрим достаточность этих решений:

Если a = 2, то система примет вид: $\begin{cases} 2x^2 + 1 = y - |sin x| \\ tg^2x + y^2 = 1\end{cases}$.

Обратим внимание, что из второго уравнения следует, что y ≤ 1.Значит правая часть первого уравнения y – │sinx│ ≤ 1, но левая часть того же уравнения 2x² + 1 ≥ 1, значит решение возможно, только если x = 0, и 1 = y.

Значит a = 2 ― значение параметра, при котором система имеет единственное решение (0; 1).

Если a = 0, то система примет вид: $\begin{cases} - 1 = y - |sin x| \\ tg^2x + y^2 = 1\end{cases}$.

Но sin(0) = tg(0) = sin(π) = tg(π) = 0,поэтому у системы будут как минимум три решения: (0; –1), (π; –1), (–π; –1). Значит условие a = 0 не является достаточным.

Итого, условие выполняется, только при значении 2.

Обратим внимание на нужное количество корней: нужен случай, когда корень единственный.

В таких случаях обращаем внимание на чётность функции. Подставим (-х).

$(-x)^2 + (2-a)^2 = |(-x)-2+a| + |(-x)-a+2| \\ x^2 + (2-a)^2 = |-x -2 + a| + |-x -a + 2| \\ x^2 + (2-a)^2 = |x+2-a| + |x + a - 2| \\ x^2 + (2-a)^2 = |x+a-2| + |x + 2 - a| \\ x^2 + (2-a)^2 = |x-2+a| + |x - a + 2|$

С помощью преобразований и перестановок привели данное уравнение к тому, что написано в условии. Значит, если 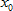является корнем уравнения, тогда и - 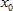является корнем.

Значит, уравнение будет иметь нечетное число корней (в том числе единственный корень) только тогда, когда он равен 0.

Подставим 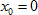в уравнение.

Будем решать это уравнение как обычное уравнение с модулем.

$0^2 + (2-a)^2 = |0-2+a| + |0-a+2| \\ (2-a)^2 = |-2 + a| + |-a + 2| \\ (2-a)^2 = |a-2| + |2-a| \\ (a-2)^2 = |a-2| + |a-2| \\ (a-2)^2 = 2|a - 2| \\ (a -2 )^2 - 2|a - 2| = 0 \\ |a-2|(|a-2| - 2) = 0 \rightarrow \begin{cases} |a-2| = 0 \\ |a-2| = 2 \end{cases} \rightarrow \begin{cases} a = 2 \\ a = 4 \\ a = 0 \end{cases}$

Подставим эти значения в изначальное уравнение и проверим.

$x^2 + (2-a)^2 = |x - 2 + a| + |x-a + 2| \\ a = 2 \\ x^2 + (2-2)^2 = |x-2+2| + |x-2+2| \\ x^2 = |x| + |x| \\ x^2 = 2|x| \\ x^2 - 2|x| = 0 \\ |x|(|x| - 2) = 0 \rightarrow \begin{cases} x = 0 \\ x = 2 \\ x = -2 \end{cases}$

Уравнение имеет три корня.

$a = 4 \\ x^2 + (2-4)^2 = |x - 2+4| + |x - 4 +2| \\ x^2 + 4 = |x + 2| + |x - 2| \\ \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 + 4 = -x - 2 - x + 2\end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 + 4 = x + 2 - x + 2\end{cases} \\ \begin{cases} x > 2 \\ x^2 + 4 = x + 2 + x - 2\end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 +2x +4 = 0 \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \\ \begin{cases} x > 2 \\ x^2 -2x +4 = 0 \end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ \oslash \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \rightarrow x = 0\\ \begin{cases} x > 2 \\ \oslash \end{cases} \end{cases}$

Уравнение имеет один корень.

$a = 0 \\ x^2 + (2-0)^2 = |x - 2+0| + |x - 0 +2| \\ x^2 + 4 = |x - 2| + |x + 2| \\ x^2 + 4 = |x + 2| + |x - 2| \\ \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 + 4 = -x - 2 - x + 2\end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 + 4 = x + 2 - x + 2\end{cases} \\ \begin{cases} x > 2 \\ x^2 + 4 = x + 2 + x - 2\end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 +2x +4 = 0 \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \\ \begin{cases} x > 2 \\ x^2 -2x +4 = 0 \end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ \oslash \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \rightarrow x = 0\\ \begin{cases} x > 2 \\ \oslash \end{cases} \end{cases}$

Уравнение имеет один корень.

Итак, уравнение имеет один корень при а=0 и а=4.

Проверим данное уравнение на чётность, подставив корень х=-х.

$(-x)^4 + (a-3)^2 = |(-x) -a + 3| + |(-x) + a - 3| \\ x^4 + (a-3)^2 = |-x -a + 3| + |-x +a-3| \\ x^4 + (a-3)^2 = |x+a-3| + |x-a+3| \\ x^4 + (a-3)^2 = |x-a+3| + |x+a - 3| $
С помощью преобразований и перестановок привели данные уравнения к тому, что написано в условии. Значит, если $x_0$ является корнем уравнения, тогда и $-x_0$ является корнем. Значит, уравнение будет иметь нечетное число корней (в том числе единственный корень) только тогда, когда он равен 0.
Подставим $x_0 = 0$ в уравнение.
$0^4 + (a-3)^2 = |0-a+3| + |0+a-3| \\ (a-3)^2 = |-a+3| + |a-3| \\ (a-3)^2 = |a-3| + |a-3| \\ (a-3)^2 = 2|a-3| \\ (a-3)^2 - 2|a-3| = 0 \\ \rightarrow \begin{cases} |a - 3| = 0 \\ |a-3| = 2 \end{cases} \rightarrow \begin{cases} a - 3 = 0 \\ a-3 = 2 \\ a-3 = -2 \end{cases} \rightarrow \begin{cases} a = 3\\ a = 5 \\ a = 1 \end{cases} \rightarrow$

Подставим эти значения в уравнение.

$a = 3 \\ x^4 + (3-3)^2 = |x - 3 +3| + |x +3 -3| \\ x^4 = |x| + |x| \\ x^4 = 2|x| \\ x^4 - 2|x| = 0 \\ |x|(|x|^3 - 2) = 0 \rightarrow \begin{cases} x = 0 \\ x = 2^{\displaystyle \frac{1}{3}} \\ x = -2^{\displaystyle \frac{1}{3}} \end{cases} $

Уравнение имеет три корня, что не подходит по условию.

$a = 5 \\ x^4 + (5-3)^2 = |x-5+3| + |x + 5 -3| \\ x^4 + 4 = |x-2| + |x+2| \\ \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 + 4 = -x - 2 - x + 2\end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 + 4 = x + 2 - x + 2\end{cases} \\ \begin{cases} x > 2 \\ x^2 + 4 = x + 2 + x - 2\end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 +2x +4 = 0 \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \\ \begin{cases} x > 2 \\ x^2 -2x +4 = 0 \end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ \oslash \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \rightarrow x = 0\\ \begin{cases} x > 2 \\ \oslash \end{cases} \end{cases}$

Уравнение имеет один корень.

$a = 1 \\ x^4 + (1-3)^2 = |x-1+3| + |x + 1 -3| \\ x^4 + 4 = |x-2| + |x+2| \\ \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 + 4 = -x - 2 - x + 2\end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 + 4 = x + 2 - x + 2\end{cases} \\ \begin{cases} x > 2 \\ x^2 + 4 = x + 2 + x - 2\end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 +2x +4 = 0 \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \\ \begin{cases} x > 2 \\ x^2 -2x +4 = 0 \end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ \oslash \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \rightarrow x = 0\\ \begin{cases} x > 2 \\ \oslash \end{cases} \end{cases}$

Уравнение имеет один корень.

Итак, нашли 2 граничных значения: 1 и 5. В них единственный корень.

Обратим внимание на нужное количество корней: нужен случай, когда корень единственный.

В таких случаях обращаем внимание на чётность функции. Подставим (-х).

$(-x)^2 + (a+4)^2 = |(-x) -4-a| + |(-x) +a+4| \\ x^2 +(a+4)^2 = |-x-4-a| + |-x+a+4| \\ x^2 + (a+4)^2 = |x+4+a| + |x-a-4| \\ x^2 + (a+4)^2 = |x-a-4| + |x + 4+a| \\ x^2 +(a+4)^2 = |x-4-a| + |x+a+4|$

С помощью преобразований и перестановок привели данное уравнение к тому, что написано в условии. Значит, если x₀ является корнем уравнения, тогда и - x₀ является корнем.

Значит, уравнение будет иметь нечетное число корней (в том числе единственный корень) только тогда, когда он равен 0.

Подставим $x_0 = 0$ в уравнение.

Будем решать это уравнение как обычное уравнение с модулем.

$0^2 + (a+4)^2 = |0-4-a| + |0+a+4| \\ (a + 4)^2 = |-4-a| + |a+4| \\ (a+4)^2 = |a+4| + |a+4| \\ (a+4)^2 = 2|a+4| \\ (a+4)^2 - 2|a+4| = 0 \\ \rightarrow \begin{cases} |a+4| = 0 \\ |a+4| = 2 \end{cases} \rightarrow \begin{cases} a = -4 \\ a = -2 \\ a = -6 \end{cases}$

Подставим эти значения в изначальное уравнение и проверим.

$x^2 + (a+4)^2 = |x-4-a| + |x+a+4| \\ a = -4 \\ x^2 + (-4+4)^2 = |x-4+4| + |x-4+4| \\ x^2 = |x| + |x| \\ x^2 = 2|x| \\ x^2 - 2|x| = 0 \\ |x|(|x| - 2) = 0 \rightarrow \begin{cases} x = 0 \\ x = 2 \\ x = -2 \end{cases}$

Уравнение имеет три корня.

$a = -2 \\ x^2 + (-2+4)^2 = |x-4+2| + |x -2 +4| \\ x^2 + 4 = |x-2| + |x+2| \\ \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 + 4 = -x - 2 - x + 2\end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 + 4 = x + 2 - x + 2\end{cases} \\ \begin{cases} x > 2 \\ x^2 + 4 = x + 2 + x - 2\end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 +2x +4 = 0 \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \\ \begin{cases} x > 2 \\ x^2 -2x +4 = 0 \end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ \oslash \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \rightarrow x = 0\\ \begin{cases} x > 2 \\ \oslash \end{cases} \end{cases}$

Уравнение имеет один корень.

$a = -6 \\ x^2 + (-6+4)^2 = |x-4+6| + |x -6 +4| \\ x^2 + 4 = |x-2| + |x+2| \\ \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 + 4 = -x - 2 - x + 2\end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 + 4 = x + 2 - x + 2\end{cases} \\ \begin{cases} x > 2 \\ x^2 + 4 = x + 2 + x - 2\end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ x^2 +2x +4 = 0 \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \\ \begin{cases} x > 2 \\ x^2 -2x +4 = 0 \end{cases} \end{cases} \rightarrow \begin{cases} \begin{cases} x < -2 \\ \oslash \end{cases} \\ \begin{cases} -2 \leq x \leq 2 \\ x^2 = 0 \end{cases} \rightarrow x = 0\\ \begin{cases} x > 2 \\ \oslash \end{cases} \end{cases}$

Уравнение имеет один корень.

Итак, уравнение имеет один корень при а = -2 и а = -6.

$f(x) = 4x^2 -4ax + a^2 +2a + 2 \\ f'(x) =8x -4a$

$f'(x) = 0 \rightarrow 8x -4a = 0 \rightarrow 8x = 4a \rightarrow x=\displaystyle \frac{1}{2} a$- точка экстремума.

Так как $f(x) = 4x^2 -4ax + a^2 +2a + 2$ - квадратичная функция, у которой только одна точка экстремума, и она находится в вершине параболы, следовательно, глобально наименьшее значение функции достигается в точке $x = \displaystyle \frac{1}{2}a$.

Найдём значение функции в этой точке:

$f(\displaystyle \frac{a}{2}) = 4(\displaystyle \frac{a}{2})^2 -4a(\displaystyle \frac{a}{2}) + a^2 + 2a+2 = 4\displaystyle \frac{a^2}{4} - 4\displaystyle \frac{a^2}{2} + a^2 +2a + 2 = a^2 -2a^2 +a^2 + 2a + 2 = 2a + 2$

Необходимо найти наименьшее значение функции на множестве $|x| \geq 1$.

$|x| \geq 1 \leftrightarrow \begin{cases} x \geq 1 \\ x \leq -1\end{cases}$

Тогда мы понимаем, что это значение достигается либо в точке $x = \displaystyle \frac{1}{2}a$, либо в точке 1, либо в точке -1.

Также требуется, чтобы наименьшее значение функции было не меньше 6, значит, на заданном промежутке все значения функции не меньше 6, в том числе и в граничных точках:

$\begin{cases}f(1) =4\cdot 1 -4a\cdot1 + a^2 + 2a + 2 \geq 6 \\ f(-1) = 4\cdot(-1)^2 - 4a\cdot(-1) + a^2 + 2a + 2 \geq 6 \end{cases} \rightarrow \begin{cases}f(1) =4 -4a + a^2 + 2a + 2 \geq 6 \\ f(-1) = 4+ 4a + a^2 + 2a + 2 \geq 6 \end{cases} \rightarrow \begin{cases}f(1) = a^2 - 2a \geq 0 \\ f(-1) = a^2 + 6a \geq 0 \end{cases} \rightarrow \begin{cases}f(1) = a(a-2) \geq 0 \\ f(-1) = a(a+6) \geq 0 \end{cases} \rightarrow \begin{cases} \begin{cases} a\leq 0 \\ a \geq 2 \end{cases} \\ \begin{cases} a \leq -6 \\ a \geq 0 \end{cases} \end{cases} \rightarrow \begin{cases} a \leq -6 \\ a \geq 2 \\ a = 0 \end{cases}$

Рассмотрим все три случая отдельно.

Если $a \leq -6$:

$x = \displaystyle \frac{1}{2}a \leq \displaystyle \frac{1}{2}\cdot (-6) = -3 \rightarrow x \leq -3$, то есть наименьшее значение функции достигается в точке $x = \displaystyle \frac{1}{2}a$.

$f(\displaystyle \frac{a}{2}) = 2a + 2 \leq 2\cdot (-6) + 2 \\ f(\displaystyle \frac{a}{2}) \leq -10$

В этих точках наименьшее значение функции меньше -10 и тем более меньше 6, что не удовлетворяет условию.

Если :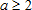

$x = \displaystyle \frac{1}{2}a \geq \displaystyle \frac{1}{2}\cdot 2 \rightarrow x \geq 1$, то есть наименьшее значение функции достигается в точке $x = \displaystyle \frac{1}{2}a$.

$f(\displaystyle \frac{a}{2}) = 2a + 2 \geq 2\cdot 2 + 2 \\ f(\displaystyle \frac{a}{2}) \geq 6$

В этих точках наименьшее значение функции не меньше 6, что удовлетворяет условию.

Если a=0:

$f(x) = 4x^2 + 2 = 2(2x^2 + 1) = 4(x^2 + \displaystyle \frac{1}{2})$

Наименьшее значение достигается в точке $x = \displaystyle \frac{1}{2}a = 0$, что не лежит в промежутке из условия. Тогда либо в точке 1, либо в точке -1.

$f(1) = 4(1^2 + \displaystyle \frac{1}{2}) = 6$, что подходит по условию.

$f(-1) = 4((-1)^2 + \displaystyle \frac{1}{2}) = 6$, что подходит по условию.

Таким образом, нужные значения параметра – это все 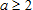и 0.

$f(x) = 4x^2 +4ax + a^2 -2a + 2 \\ f'(x) =8x +4a$
$f'(x) = 0 \rightarrow 8x +4a = 0 \rightarrow 8x = -4a \rightarrow x=-\displaystyle \frac{1}{2} a$- точка экстремума.

Так как $f(x) = 4x^2 +4ax + a^2 -2a + 2$ - квадратичная функция, у которой только одна точка экстремума, и она находится в вершине параболы, следовательно, глобально наименьшее значение функции достигается в точке $x = -\displaystyle \frac{1}{2}a$.

Найдём значение функции в этой точке:

$f(-\displaystyle \frac{a}{2}) = 4(-\displaystyle \frac{a}{2})^2 +4a(-\displaystyle \frac{a}{2}) + a^2 - 2a+2 = 4\displaystyle \frac{a^2}{4} - 4\displaystyle \frac{a^2}{a} + a^2 -2a + 2 = a^2 -2a^2 +a^2 - 2a + 2 = -2a + 2$

Необходимо найти наименьшее значение функции на множестве $|x| \geq 1$..

$|x| \geq 1 \leftrightarrow \begin{cases} x \geq 1 \\ x \leq -1\end{cases}$

Тогда мы понимаем, что это значение достигается либо в точке $x = -\displaystyle \frac{1}{2}a$, либо в точке 1, либо в точке -1.

Также требуется, чтобы наименьшее значение функции было не меньше 6, значит, на заданном промежутке все значения функции не меньше 6, в том числе и в граничных точках:

$\begin{cases}f(1) =4\cdot 1 +4a\cdot1 + a^2 - 2a + 2 \geq 6 \\ f(-1) = 4\cdot(-1)^2 + 4a\cdot(-1) + a^2 - 2a + 2 \geq 6 \end{cases} \rightarrow \begin{cases}f(1) =4 +4a + a^2 - 2a + 2 \geq 6 \\ f(-1) = 4-4a + a^2 - 2a + 2 \geq 6 \end{cases} \rightarrow \begin{cases}f(1) = a^2 + 2a \geq 0 \\ f(-1) = a^2 - 6a \geq 0 \end{cases} \rightarrow \begin{cases}f(1) = a(a+2) \geq 0 \\ f(-1) = a(a-6) \geq 0 \end{cases} \rightarrow \begin{cases} \begin{cases} a\leq -2 \\ a \geq 0 \end{cases} \\ \begin{cases} a \leq 0 \\ a \geq 6 \end{cases} \end{cases} \rightarrow \begin{cases} a \leq -2 \\ a \geq 6 \\ a = 0 \end{cases}$

Рассмотрим все три случая отдельно.

Если $a \leq -2$:

$x = -\displaystyle \frac{1}{2}a \geq -\displaystyle \frac{1}{2}\cdot (-2) = 1 \rightarrow x \geq 1$, то есть наименьшее значение функции достигается в точке

$x = -\displaystyle \frac{1}{2}a$

$f(-\displaystyle \frac{a}{2}) = -2a + 2 \geq 2\cdot (-2) + 2 \\ f(-\displaystyle \frac{a}{2}) \geq 6$

В этих точках наименьшее значение функции не меньше 6, что удовлетворяет условию.

Если $a \geq 6$:

$x = -\displaystyle \frac{1}{2}a \leq -\displaystyle \frac{1}{2}\cdot 6 \rightarrow x \leq -3$

$x = -\displaystyle \frac{1}{2}a$

$f(-\displaystyle \frac{a}{2}) =- 2a + 2 \leq -2\cdot 6 + 2 \\ f(-\displaystyle \frac{a}{2}) \leq -10$

В этих точках наименьшее значение функции меньше -10 и тем более меньше 6, что не удовлетворяет условию.

Если a = 0:

$f(x) = 4x^2 + 2 = 2(2x^2 + 1) = 4(x^2 + \displaystyle \frac{1}{2})$

Наименьшее значение достигается в точке $x = -\displaystyle \frac{1}{2}a = 0$, что не лежит в промежутке из условия. Тогда либо в точке 1, либо в точке -1.

$f(1) = 4(1^2 + \displaystyle \frac{1}{2}) = 6$, что подходит по условию.

$f(-1) = 4((-1)^2 + \displaystyle \frac{1}{2}) = 6$, что подходит по условию.

Таким образом, нужные значения параметра – это все $a \leq -2$ и 0.