Запишем уравнение в виде │x² – 2x – 3│ = │x – a│ + 2a – 1.

Построим график функции y = │x² – 2x – 3│ и график функции y = │x – a│ + 2a – 1. Из рисунка видно, что подходящих значений a ровно два ― при одном из них график правой части проходит через точку (–1; 0) при другом ― касается отражённого участка параболы.

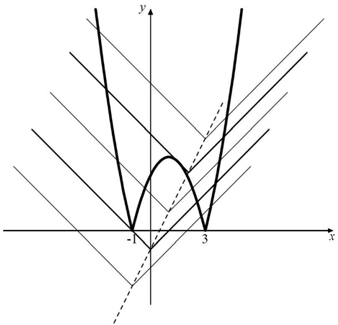
Первое, очевидно, происходит при a = 0, а второе ― когда уравнение 3 + 2x – x² = 3a – 1 – x имеет единственный корень. Приравнивая дискриминант к нулю, находим a = $\displaystyle \frac {25}{12}$.

Преобразуем систему: $\left\{ \begin{array}{l} -14\leq 3x-y\leq 10 \\ (x-3a)^{2}+(y+a)^{2}=3a+4 \end{array} \right. $

Неравенство –14 ≤ 3x – y ≤ 10 задаёт на плоскости полосу, граница которой ― пара параллельных прямых: 3x – y = – 14 и 3x – y = 10.

Если a < $\displaystyle \frac {4}{3}$, то система не имеет решений, поскольку правая часть второго уравнения становится отрицательной. Если a = –$\displaystyle \frac {4}{3}$, то уравнение принимает вид $(x+4)^{2}+\left( y-\displaystyle \frac{4}{3}\right) ^{2}=0$ и задает единственную точку $\left( -4;\displaystyle \frac{4}{3}\right) $, координаты которой удовлетворяют неравенству $\left\vert -12-\displaystyle \frac{4}{3}+2\right\vert =\displaystyle \frac{34}{3} < 12$

Следовательно, при a = –$\displaystyle \frac {4}{3}$ система имеет единственное решение.

Рассмотрим случай a > –$\displaystyle \frac {4}{3}$.

Тогда уравнение (x – 3a)² + (y + a)² = 3a + 4 определяет окружность радиусом $r=\sqrt{3a+4}$.

Центр M (3a; –a) окружности лежит на прямой $y=-\displaystyle \frac{1}{3}x$ ,

Прямые $y=-\displaystyle \frac{1}{3}x$ и $y=3x$ перпендикулярны, так как $k_{1}k_{2}=-1$ ($k_{1},k_{2}$ - коэффициент при $x$).

Зачит, $y=-\displaystyle \frac{1}{3}x$ перепендикуляр на и граничн ым прямым полосы и пересекает их в точках $A(-4,2;1,4)$ и $B(3;-1).$ Действительно:

$\begin{array}{ll} -\displaystyle \frac{1}{3}x=3x-10, & -\displaystyle \frac{1}{3}x=3x+14 \\ x=3,y=-1; & x=-4,2;y=1,2\end{array}$

Система имеет единственное решение, если только окружность касается полосы в точке A или в точке B внешним образом.

Точка A не подходит так как тогда:

$(4,2+3a)^{2}+(1,4+a)^{2}=3a+4$

$10a^{2}+8,2a+15,6=0$

$D<0$

Пусть окружность касается полосы в точке B, только если а > 1 (при таком a центр окружности лежит в точке (3; -1), то есть на границе области). Получаем:

(3 – 3a)² + (–1 + a)² = 3a + 4;

10a² – 23a + 6 = 0.

Корни: а = 2, а = 0,3.

Условию а > 1 удовлетворяет только первый корень.

Тогда получаем 2 варианта: –$\displaystyle \frac{4}{3}$, 2.

Способ 1. Первое уравнение системы является уравнением окружности с центром в начале координат и радиусом 2. Второе уравнение ― уравнение пучка прямых, проходящих через точку А (0; –4) (рис. 1).

Единственное решение системы уравнений (2) будет иметь при a = ±a^•, когда прямая y = ax – 4 касается окружности

x² + y² = 4. Поскольку a = tgα, то из прямоугольного треугольника ОВА находим: $tg\alpha =\displaystyle \frac{AB}{OB},$ , но OB = 2, $AB=\sqrt{OA^{2}-OB^{2}},$, $AB=\sqrt{16-4}=2\sqrt{3}$ и потому tgα = √3.

Очевидно, что при a < –√3 и a > √3 система (2) будет иметь два решения (прямая АВ будет пересекать окружность в двух точках).

Способ 2. Значения параметра (±a^•), при которых прямая y = ax – 4 является касательной к окружности, находим из условия касания графиков функций y₁(x) и y₂(x): $\left\{ \begin{array}{l} y_{1}(x)=y_{2}(x) \\ y_{1}^{\prime }(x)=y_{2}^{\prime }(x) \end{array} \right. ,$ где <$y_{1}(x)=-\sqrt{4-x^{2}}$; y₂(x) = ax – 4. Имеем $\left\{ \begin{array}{l} -\sqrt{4-x^{2}}=ax-4, \\ \displaystyle \frac{x}{\sqrt{4-x^2}}=a. \end{array} \right. $ (3).

Заменяя в первом уравнении а на $\displaystyle \frac{x}{\sqrt{4-x^{2}}}$ , получаем $-\sqrt{4-x^{2}}=\displaystyle \frac{x^{2}}{\sqrt{4-x^{2}}}-4$. Решая это уравнение, находим x = ±√3 и из второго уравнения системы (3) ― a^• = ±√3. Значения параметра а, при которых система уравнений (2) имеет более одного решения (два решения ― см. рис. 1), лежат на лучах (–∞; –√3) и (√3; +∞).

Способ 3. Значения параметра a, при которых система уравнений (2) имеет единственное решение, могут быть найдены из условия единственности решения уравнения x² + (ax – 4)² = 4 ⇔ x²(1 + a²) – 8ax + 12 = 0.

Поскольку это квадратное уравнение относительно переменной x с коэффициентом 1 + a² ≠ 0 при x², то единственное решение это уравнение будет иметь тогда и только тогда, когда D_x = 0 ⇔ 64a² – 48(1 + a²) = 0 ⇒ a^* = ±√3.

Получаем искомые значения параметра: a ∈ (―∞; ―√3) ∪ (√3; +∞).

Преобразуем систему: $\left\{ \begin{array}{l} -12\leq x+2y\leq 10 \\ (x-a)^{2}+(y-2a)^{2}=2+a \end{array} \right. $. Неравенство –12 ≤ x + 2y ≤ 10 задаёт на плоскости полосу, граница которой ― пара параллельных прямых: x + 2y = 10 и x + 2y = –12.

Если a < –2, то система не имеет решений, поскольку часть уравнения становится отрицательной. Если a = –2, то уравнение принимает вид (x + 2)² + (y + 4)² = 0 и задает единственную точку (–2; –4), координаты которой удовлетворяют неравенству │–2 – 8 + 1│ = 9 < 11.

Следовательно, при a = –2 система имеет единственное решение.

Рассмотрим случай a > –2. Тогда уравнение (x – a)² + (y – 2a)² = 2 + a определяет окружность радиусом $r=\sqrt{2+a}$.

Центр M (a; 2a) окружности лежит на прямой y = 2x, которая перпендикулярна граничным прямым, так как $k_{1}k_{2}=2\cdot \left( -\displaystyle \frac{1}{2}\right) =-1$. Границы полосы пересекаются с этой прямой в точках A (–2,4; –4,8) и B (2; 4).

$ \begin{array}{ll} \left\{ \begin{array}{l} x+2y=10 \\ y=2x \end{array} \right. & \left\{ \begin{array}{l} x+2y=10 \\ y=2x \end{array} \right. \\ \left\{ \begin{array}{l} x+2y=-12 \\ y=2x \end{array}\right. & \left\{ \begin{array}{l} x=-2,4 \\ y=-4,8 \end{array} \right. \end{array} $

Система имеет единственное решение, если только окружность касается полосы в точке A или в точке B внешним образом. Если точка касания A, то a < –2,4, что невозможно.

Окружность касается полосы в точке B, только если а > 2 и MB = r. Получаем: (a – 2)² + (2a –4)² = 2 + a, 5a² – 21a + 19 = 0. Корни: а = 3, а = 1,2.

Условию а > 2 удовлетворяет только корень а = 3.

Итого получаем значения -2 и 3.

Преобразуем наше уравнение.

$\sqrt{-7-8x-x^{2}}=2a+3-ax$

Разобьем на две функции:

$y=\sqrt{-7-8x-x^{2}}$ и $g=2a+3-ax$

Поработаем с каждой функцией отдельно.

$y=\sqrt{-7-8x-x^{2}}\leftrightarrow \left\{ \begin{array}{l} y\geq 0 \\ y^{2}=-7-8x-x^{2} \end{array} \right. \leftrightarrow \left\{ \begin{array}{l} y\geq 0 \\ y^{2}+7+8x+x^{2}=0 \end{array} \right. \leftrightarrow \left\{ \begin{array}{l} y\geq 0 \\ y^{2}+x^{2}+8x+16-9=0 \end{array} \right. \leftrightarrow $

$\leftrightarrow \left\{ \begin{array}{l} y\geq 0 \\ y^{2}+(x+4)^{2}=9 \end{array} \right. \leftrightarrow \left\{ \begin{array}{l} y\geq 0 \\ (x+4)^{2}+y^{2}=9 \end{array} \right. $

$y=\sqrt{-7-8x-x^{2}}$ - уравнение полуокружности с центром в точке $(-4;0)$ и радиусом 3.

$g=2a+3-ax$

$g=-ax+2a+3$

$g=a(2-x)+3$

$g=-ax+2a+3$– пучок прямых, проходящих через точку (2;3).

Нам необходим единственный корень.

Заметим, что если прямая $g=-ax+2a+3$ проходит через точку (-1;0) (1 случай), то только одно пересечение. Также одно решение в точке (-4;3) (2 случай), когда прямая касается окружности.

Также будет по одному пересечению т точки (-7;0) до точки (-1;0), исключая концы (3 случай).

Рассмотрим все эти случаи.

Объединяем полученные ответы.

Итого получаем значения: $0;(-\displaystyle \frac{1}{3};1]$.

Преобразуем неравенство:

a + │a + 1 – x│ ≤ 3x – x² – 1;

│x – (a + 1) │ ≤ 3x – x² – a – 1;

$\left\{ \begin{array}{l} x-a-1\leq 3x-x^{2}-a-1 \\ x-a-1\geq -3x+x^{2}+a+1 \end{array} \right. $

$\left\{ \begin{array}{l} x(x-2)\leq 0 \\ a\leq -\displaystyle \frac{1}{2}x^{2}+2x-1 \end{array} 0\right. $

Неравенство x (x – 2) < 0 определяет на плоскости Oxa полосу, заключённую между прямыми x = 0 и x = 2.

Неравенство $a\leq \displaystyle \frac{1}{2}x^{2}+2x-1$ задаёт часть плоскости, ограниченную сверху параболой.

На рисунке видно, что на отрезке [0; 1] есть x, удовлетворяющие неравенству, только если a ≤ 0,5.

Преобразуем неравенство: $a+\sqrt{a^{2}-2ax+x^{2}}\leq 3x-x^{2}$ ; │x – a│ ≤ 3x – x² – a.

$\left\{ \begin{array}{l} x-a\leq 3x-x^{2}-a, \\ x-a\geq -3x+x^{2}+a; \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x(x-2)\leq 0, \\ a\leq -\displaystyle \frac{1}{2}x^{2}+2x. \end{array} \right. $

Неравенство x(x – 2) ≤ 0 определяет на плоскости Oxa полосу, заключённую между прямыми x = 0 и x = 2. Неравенство $a\leq -\displaystyle \frac{1}{2}x^{2}+2x$ задает часть плоскости, ограниченную сверху параболой.

На рисунке видно, что на интервале (1; 2) есть х, не удовлетворяющий неравенству, только если a > 1,5.

Ясно, что прямые семейства y – 2 = k(x + 1) переходят друг в друга преобразованием поворота с центром в точке А (–1; 2). Данная система имеет решение, если указанные прямые имеют с графиком функции y = √x хотя бы одну общую точку. Имеются два предельных значения k₁ и k₂. Первая прямая касается графика y = √x. Прямые, угловой коэффициент которых удовлетворяет неравенству k₁ ≤ k ≤ k₂, имеют общую точку с «полупараболой».

Найдём значение k₁, подставив для этого в уравнение y – 2 = k(x + 1) координаты вершины (0; 0). Получаем k₁ = –2.

Значение k₂ получим из выполнения условия единственности решения смешанной системы $\left\{ \begin{array}{l} y-2=k(x+1) \\ y^{2}=x \\ k>0 \end{array} \right. $.

Это означает, что уравнение ky² – y + k + 2 = 0 имеет решение, т. е. дискриминант этого квадратного уравнения равен нулю.

D = 1 – 4k² – 8k = 0, если k = –1 + √1,25.

Тогда получаем искомые значения: –2 ≤ k ≤ –1 + √1,25.

Выполним построения на плоскости Оха.

Преобразуем систему неравенств к виду $\left\{ \begin{array}{l} a\leq x+1 \\ x^{2}-3x+1\leq a \end{array} \right. $.

Решением первого неравенства является множество точек плоскости, лежащих ниже прямой a = x + 1 (включая точки прямой), для второго ― выше параболы a = x² – 3x + 1 (включая точки параболы).

Система неравенств имеет решения при тех значениях а, при которых прямая a = const, параллельная оси Ох, имеет общие точки с заштрихованной областью. Только две прямые вида a = const, проходящие через точки А и В, имеют единственную общую точку с этой областью. Значение ординаты точки А равно –$\displaystyle \frac {5}{4}$.

Так как В ― точка пересечения графиков функций a = x² – 3x + 1 и a = x + 1, то для нахождения её абсциссы нужно решить уравнение x + 1 = x² –3x + 1 или x² – 4x = 0. Его корнями являются числа x₁ = 0 и x₂ = 4. Точке В соответствует второй корень. Соответственно, ордината точки В равна 5.

При a < $–\displaystyle \frac {5}{4}$ и a > 5 система не имеет решений.

Тогда нужные нам значения параметра - это –$\displaystyle \frac {5}{4}$ и 5.

Построим график функции y = │x² – 4x + 3│ + 1.

Построение проведём в три этапа $\Gamma _{y=x^{2}-4x+3}\rightarrow \Gamma _{\left\vert y\right\vert }\rightarrow \Gamma _{\left\vert y\right\vert +1}$. Функция y = log_ax задаёт семейство кривых, имеющих одну общую точку А (1; 0). График функции y = │x² – 4x + 3│ + 1 имеет только одну общую точку с той кривой семейства y = log_ax при a > 1, которая проходит через точку В (3; 1).

Подставив координаты точки В в соотношение y = log_ax, получим равенство 1 = log_a3, возможное при a = 3.

Так как по условию a > 1, то это единственное подходящее значение.

Корни данного уравнения должны удовлетворять условию x ≥ –2a² (условие существования квадратного корня из выражения x + 2a²).

Заметим, что x² + (2 – a)x – 2a = (x – a)(x + 2). Тогда <$\sqrt{x+2a^{2}}(x-a)(x+2)=0\Leftrightarrow \left\{ \begin{array}{l} x\geq -2a^{2} \\ \left[ \begin{array}{l} x=-2a^{2} \\ x=a \\ x=-2 \end{array} \right.\end{array} \right. $.

Следовательно, корнями уравнения могут быть числа x₁ = –2a², x₂ = a и x₃ = –2. По условию задачи требуется найти значения параметра а, при которых уравнение имеет ровно два различных корня. Для отбора искомых значений параметра на плоскости Оха построим графики функций x = –2a², x = a и x = –2. Каждая прямая a = const, параллельная оси Ох, пересекает каждый из построенных графиков, и ордината точки пересечения даёт значение корня исходного уравнения при условии, что x ≥ –2a². Имеется пять критических положений этих прямых a₁ = –2, a₂ = –1, a₃ = –0,5, a₄ = 0 и a₅ = 1. Они проходят через точки пересечения графиков. Точки –2, –1, –0,5, 0 и 1 разбивают числовую прямую Оа на шесть промежутков. Рассмотрим каждый из них: (1) a ∈ (–∞; –2) и (2) a ∈ (–2; –1). На этих промежутках уравнение имеет три корня.

a ∈ (–1; –0,5), уравнение имеет два корня (график функции x = –2 расположен ниже графика функции x = –2a²).

a ∈ (–0,5; 0), уравнение имеет один корень, так как графики функций x = a и x = –2 ― ниже графика функции x = –2a².

a ∈ (0; 1), уравнение имеет два корня (график функции x = –2 ― ниже графика функции x = –2a²).

a ∈ (1; +∞), уравнение имеет три корня.

Соответственно при a₁ = –2, a₂ = –1 и a₅ = 1 уравнение имеет два корня.

Нужные нам значения: a ∈ {–2} ⋃ [–1; –0,5) ⋃ (0; 1].