


0
из 5Решил заданий
0
из 5Не решил заданий
5
из 5Осталось заданий
Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие "буква" - "цифра" должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Многоугольники
5 заданийВ равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB=5, AC=8.
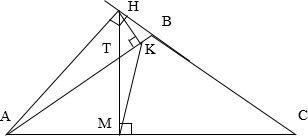
Пусть $\angle BAC=\angle BCA=\alpha .$ Тогда $\angle ABC=180^{\circ }-2\alpha .$
$\angle HBA=180^{\circ }-180^{\circ }+2\alpha =2\alpha $ как смежный с $\angle ABC.$
Так как треугольник $AHB$ - прямоугольный, то $\angle HAB=90^{\circ }-2\alpha .$
$\angle HAC=\angle HAB+\angle BAC=90^{\circ }-\alpha .$
Так как треугольник $AHM$ - прямоугольный, то $\angle AHM=90^{\circ }-90^{\circ }+\alpha =\alpha .$
Аналогично из прямоугольго треугольника $HKB$ получаем, что $\angle BHK=90^{\circ}-2\alpha .$
Рассмотрим $\angle AHB=90^{\circ }=\angle AHM+\angle THK+\angle BHK=\alpha +\angle THK+90^{\circ }-2\alpha \Rightarrow \angle THK=\alpha .$
В треугольниках $ATM$ и $HTK$ $\angle TAM=\angle THK$ по доказанному, $\angle AMT=\angle HKT=90^{\circ }$ по условию. Значит, данные треугольники подобны по призкаку подобия по 2 углам. Следовательно,
$\displaystyle \frac{KT}{TM}=\displaystyle \frac{HT}{AT}\Rightarrow \displaystyle \frac{KT}{HT}=\displaystyle \frac{TM}{AT}.$
В треугольнике $ATH$ и $MTK$ $\angle ATH=\angle MTK$ как вертикальные, $\displaystyle \frac{KT}{HT}=\displaystyle \frac{TM}{AT}$ по доказанномую Значит, данные треугольники подобны по 2 пропорциональнымсторонам и углу между ними. Тогда, $\angle AHT=\angle TKM=\alpha .$
Получили, что в треугольнике $AKM$ углы при стороне $AK$ равны, значит, треугольник - равнобедренный и $AM=KM.$
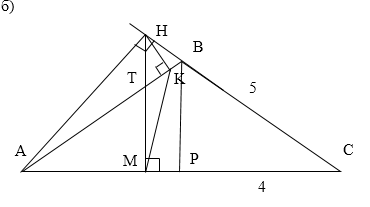
Проведем прямую $BP//HM.$ В равнобедренном треугольнике $ABC$ отрезок $BP$ будет являться высотой и медианой, поэтому $PC=4.$ По теорем е Пифагора $BP^{2}=\sqrt{BC^{2}-PC^{2}}=3.$
Прямая $BP$ отсекает от треугольника $HCM$ подобные ему треугольник $BCP,$ поэтому $\displaystyle \frac{PC}{CM}=\displaystyle \frac{BC}{HC},$
$\displaystyle \frac{4}{CM}=\displaystyle \frac{5}{HC}\Rightarrow HC=\displaystyle \frac{5}{4}CM.$
Обозначим $CM=x,$ тогда $HC=\displaystyle \frac{5}{4}x,$ $BH=\displaystyle \frac{5}{4}x-5,$ $AM=8-x.$
Из треугольника $ABH$ по теореме Пифагора $AH^{2}=AB^{2}-BH^{2}=25-(\displaystyle \frac{5}{4}x-5)^{2}=\displaystyle \frac{25}{2}x-\displaystyle \frac{25}{16}x^{2}.$
Аналогично из треугольника $AHC$ $AC^{2}=AH^{2}+HC^{2}$
$64=\displaystyle \frac{25}{2}x-\displaystyle \frac{25}{16}x^{2}+\displaystyle \frac{25}{16}x^{2}$
$x=\displaystyle \frac{128}{25}$
$KM=AM=8-x=\displaystyle \frac{72}{25}$
Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10.
а) Докажите, что диагонали перпендикулярны.
б) Найдите высоту трапеции.
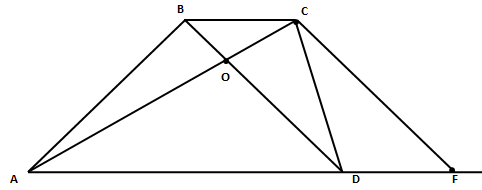
а) Проведем прямую CF//BD, тогда BCFD – параллелограмм и BC = DF, CF = BD.
В треугольнике ACF AC = 8, CF = 6, AF = AD + DF = 10.
Если диагонали перпендикулярны, то треугольник ACF – прямоугольный и выполняется теорема Пифагора:
$AC^{2}+CF^{2}=AF^{2}$
$64+36=100$
Значит, угол между диагоналями равен 90⁰.
б) $S_{ABCD}=\displaystyle \frac{BC+AD}{2}\cdot h=5h,$ , где h – длинна высоты.
С другой стороны $S_{ABCD}=\displaystyle \frac{1}{2}\cdot BD\cdot AC\cdot \sin 90^{\circ }=24$
Тогда
$5h=24$
$h=4,8$
Дана равнобедренная трапеция, в которой AD = 3BC, CM — высота трапеции.
а) Доказать, что M делит AD в отношении 2:1.
б) Найдите расстояние от точки C до середины BD, если AD = 18, $AC=4\sqrt{13}.$.
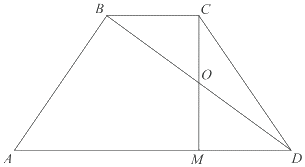
а) Поскольку ABCD — равнобедренная трапеция, то
$MD=\displaystyle \frac{AD-BC}{2}=\displaystyle \frac{3BC-BC}{2}=BC$
Тогда $AM=2BC$. Следовательно, $\displaystyle \frac{AM}{MD}=\displaystyle \frac{2}{1}$
б)
Треугольник AMC прямоугольный. В нем $AM=\displaystyle \frac{2}{3}AD=12$ по доказанному в пункте а) и $AC=4\sqrt{13}$ по условию.
По теореме Пифагора $CM^{2}+AM^{2}=AC^{2}$ , откуда $CM=8$ .
Треугольники BCO и MOD равны по катету и острому углу (BC=MD по доказанному в пункте а) , углы CBO и ADO равны как накрест лежащие). Тогда BO = OD и СO = OM как соответственные элементы равных треугольников. Значит, СO - искомое расстояние.
$CO=CO=\displaystyle \frac{CM}{2}=4$.
В остроугольном треугольнике ABC провели высоту BH из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.
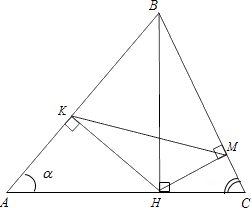
а) Обозначим $\angle BAC=\alpha .$. Треугольники AKH, CMH, ABH и BKH – прямоугольные. Тогда $\angle KHA=\angle ABH=90^{\circ }-\alpha .$. Аналогично $\angle KHB=90^{\circ }-(90^{\circ }-\alpha )=\alpha .$. В четырехугольнике BKHM $\angle BKH+\angle BMH=90^{\circ }+90^{\circ }=180^{\circ },$, значит, вокруг этого четырехугольника можно описать окружность. Углы $\angle KHB=\angle KMB=\alpha $ как опирающиеся на одну и ту же хорду.
В треугольниках ABC и MKB $\angle KMB=\angle BAC,\angle ABC$ - совпадающий. Значит, они подобны по признаку подобия по 2 углам.
б) Обозначим k – коэффициент подобия треугольников ABC и MKB (k<1).
Площади подобных фигур относятся как квадраты их линейных отношений, поэтому $\displaystyle \frac{S_{BMK}}{S_{ABC}}=k^{2}\Rightarrow S_{BMK}=k^{2}\cdot S_{ABC}$ .
Площадь фигуры равна сумме площадей ее частей, поэтому $S_{AKMC}=S_{ABC}-S_{BMK}=(1-k^{2})S_{ABC}.$ Тогда $\displaystyle \frac{S_{BMK}}{S_{AMKC}}=\displaystyle \frac{k^{2}}{1-k^{2}}.$.
Определим коэффициент подобия. Из треугольника BKH по определению $\sin \alpha =\displaystyle \frac{KB}{BH}$ . Из треугольника ABC по теореме синусов $\sin \alpha =\displaystyle \frac{BC}{2R}$ , где R – радиус описанной окружности.
$\displaystyle \frac{KB}{BH}=\displaystyle \frac{BC}{2R}\Rightarrow \displaystyle \frac{KB}{BC}=\displaystyle \frac{BH}{2R}=\displaystyle \frac{2}{2\cdot 4}=\displaystyle \frac{1}{4}$
В то же время, KB и BH – стороны, лежащие напротив одинаковых углов, в подобных треугольниках ABC и MKB. Тогда $k=\displaystyle \frac{1}{4}$.
Подставим найденное значение в отношение площадей:
$\displaystyle \frac{S_{BMK}}{S_{AMKC}}=\displaystyle \frac{k^{2}}{1-k^{2}}=\displaystyle \frac{1}{15}.$
Точки P, Q, W делят стороны выпуклого четырёхугольника ABCD в отношении AP:PB=CQ:QB=CW:WD=1:4, радиус окружности, описанной около треугольника PQW, равен 10, PQ=16, QW=12, угол PWQ — острый.
а) Докажите, что треугольник PQW — прямоугольный.
б) Найдите площадь четырёхугольника ABCD.
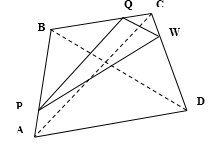
а) По теореме синусов из треугольника $PQW:$
$2R=\displaystyle \frac{PQ}{\sin \angle PWQ}=\displaystyle \frac{QW}{\sin \angle QPW},$
$20=\displaystyle \frac{16}{\sin \angle PWQ}=\displaystyle \frac{12}{\sin \angle QPW}\Rightarrow $
$\sin \angle PWQ=\displaystyle \frac{4}{5},\sin \angle QPW=\displaystyle \frac{3}{5}.$
Заметим, что $\sin ^{2}\angle PWQ+\sin ^{2}\angle QPW=\displaystyle \frac{16}{25}+\displaystyle \frac{9}{25}=1.$
Значит:
$\sin ^{2}\angle QPW=\cos ^{2}\angle PWQ,$
$\sin \angle QPW=\cos \angle PWQ,$
так как угол $QWP$ - острый. Тогда $\angle QPW+\angle PWQ=90^{\circ }$ и треугольник $PQW$ - прямоугольный.
б) Треугольник $PBQ$ и $ABC$ подобные по двум стронам и углу между ими ($\angle B$ - общий, $\displaystyle \frac{BC}{BQ}=\displaystyle \frac{AB}{BP}=\displaystyle \frac{5}{4}).$ Значит, $AC\parallel PQ$ и $AC=\displaystyle \frac{5}{4}PQ=20.$
Аналогично, из подобия треугольников $QCW$ и $BCQ$ получаем, что $BD\parallel QW$ и $BD=5QN=60$
Угол между прямыми $BD$ и $AC$ равен углу между прямыми $PQ$ и $QW,$ поэтому
$S_{ABCD}=\displaystyle \frac{1}{2}BD\cdot AC\cdot \sin 90^{\circ }=\displaystyle \frac{1}{2}60\cdot 20=600.$

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

«Выбери тест, предмет и нажми кнопку «Начать решать»

После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию

Решай задания и записывай ответы. После 1-ой попытки ты сможешь посмотреть решение

Сбоку ты можешь посмотреть статистику и прогресс по предмету

Нажми, чтобы начать решать вариант. Как только ты перейдешь на страницу, запустится счетчик времени, поэтому подготовь заранее все, что может тебе понадобиться

Отмечай те статьи, что прочитал, чтобы было удобнее ориентироваться в оглавлении

Ты прошел обучение! Теперь ты знаешь как пользоваться сайтом и можешь переходить к решению заданий