


0
из 6Решил заданий
0
из 6Не решил заданий
6
из 6Осталось заданий
Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие "буква" - "цифра" должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Окружности
6 заданийВ треугольнике ABC угол ABC равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin∠BMC, если известно, что отрезок BM в 2,5 раза больше радиуса вписанной в треугольник окружности.
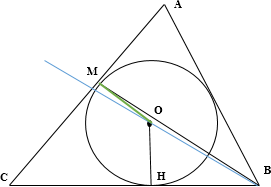
а) Проведем радиусы $OH\perp BC$ и $OM\perp AC$ с длинной $R.$ Так как центр вписанной окружности находится в точке пересечения биссектрис, то $\angle OBH=30^{\circ }.$ Катет, лежащий против угла в $30^{\circ }$ равен половине гипотенузы $\Rightarrow OB=2OH=2R.$ По неравенству треугольника для $OBM$ имеем $BM < OM+OB=3R.$
б) Запишем теорему косинусов для треугольника $OBM:$
$OB^{2}=OM^{2}-2OM\cdot BM\cos \angle BMO,$
$4R^{2}=R^{2}+6,25R^{2}-5R^{2}\cos \angle BMO,$
cos$\angle BMO=\displaystyle \frac{3,25}{5}=0,65.$
Так как $\angle OMC=90^{\circ },$ то $\sin \angle BMC=\sin (90^{\circ }+\angle BMO)=\cos \angle BMO=0,65.$
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK=3 и MK=12.

а) Треугольники $ABD$ и $BMC$ - прямоугольные, так как опираются на диаметры окружностей. Тогда $AD$ и $CM$ перпендикулярны одной и той же прямой $DM$. Следовательно, $AD\parallel MC.$
б) Пусть $O$ - центр окружности с диаметром $AB.$ Тогда отрезок $OM$ перпендикулярен $AM.$
Так как угол $AKB$ - вписанный, опирающийся на диаметр, то отрезок $KB$ перпендикулярен $AM.$ Значит, $ KB\parallel OM\ $\ и треугольники $AKB$ и $AOM$ подобны по двум углам:
$\displaystyle \frac{AK}{AM}=\displaystyle \frac{KB}{OM}=\displaystyle \frac{3}{15}=\displaystyle \frac{1}{5},$
$OM=5KB.$
Проведем высоту $BP$ в треугольнике $BOP:$
$BP^{2}+OP^{2}=OB^{2},$
$144+16KB^{2}=25KB^{2},$
$KB=4.$
Рассмотрим треугольники $ACM$ и $DCM.$ Они имеют одинаковые основания $MC$ и высоту $DM,$ а, значит, и равные площадию
$S_{DBC}=S_{DCM}-S_{BMC}=S_{AMC}-S_{BMC}=S_{AMB}=\displaystyle \frac{1}{2}AM\cdot KB=30.$
Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C1 и В1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику АВ1С1.
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45∘, В1С1 = 6 и площадь треугольника АВ1С1 в восемь раз меньше площади четырёхугольника ВСВ1С1.
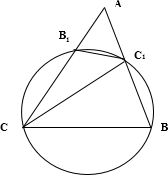
a) В треугольниках $ABC$ и $AB_{1}C_{1}$ $\angle A$ - общий. $AC$ и $AB$ - секущие, проведениные из одной точки, следовательно, $\displaystyle \frac{AB_{1}}{AB}=\displaystyle \frac{AC_{1}}{AC}.$ Тогда треугольники $ABC$ и $\ AB_{1}C_{1}$ подобны по двум сторонам и углу между ними.
б) Отношение площадей подобных фигур равно квадрату линейного отношения соответсвенных элементов данных фигур:
$S_{BCB_{1}C_{1}}=8S_{AB_{1}C_{1}},$
$S_{ABC}=S_{BCB_{1}C_{1}}+S_{AB_{1}C_{1}}=9S_{AB_{1}C_{1}},$
$\displaystyle \frac{S_{AB_{1}C_{1}}}{S_{ABC}}=\left( \displaystyle \frac{B_{1}C_{1}}{BC}\right)^{2}=\left( \displaystyle \frac{AC_{1}}{AC}\right) ^{2}=\left( \displaystyle \frac{AB_{1}}{AB}\right)^{2}=\displaystyle \frac{1}{9}\Rightarrow BC=3B_{1}C_{1}=18.$
По теореме косинусов в треугольнике $ACC_{1}:$
$CC_{1}^{2}=AC^{2}+AC_{1}^{2}+-2AC\cdot AC\ _{1}\cos \angle A,$
$CC_{1}^{2}=9AC_{1}^{2}+AC_{1}^{2}-3AC_{1}^{2}\sqrt{2},$
$CC_{1}=AC_{1}\sqrt{10-3\sqrt{2}}.$
По теореме синусов $ACC_{1}:$
$\displaystyle \frac{AC}{\sin \angle AC_{1}C}=\displaystyle \frac{CC_{1}}{\sin \angle A}\Rightarrow $
$\sin \angle AC_{1}C=\sin \angle BC_{1}C=\displaystyle \frac{AC\sin \angle A}{CC_{1}}=\displaystyle \frac{3AC_{1}}{AC_{1}\sqrt{2}\cdot \sqrt{10-3\sqrt{2}}}=\displaystyle \frac{3}{\sqrt{20-6\sqrt{2}}}.$
Искомый радиус совпадает с радиусом окружности, описанной около треугольника $BCC_{1}.$ по теореме синусов из треугольника $BCC_{1}:$
$\displaystyle \frac{BC}{\sin \angle BC_{1}C}=2R\Rightarrow R=3\sqrt{20-6\sqrt{2}}.$
В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая — боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что $\displaystyle \frac{AP}{DP}=\sin \angle D$.
б) Найдите площадь трапеции, если радиусы окружностей равны $\displaystyle \frac{4}{3}$ и $\displaystyle \frac{1}{3}$ .
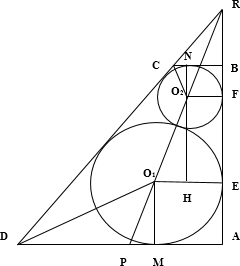
а) Продолжим стороны $AB$ и $CD$ до пересечения в точки $R$. Окружности вписаны в угол, следовательно, их центры лежат на биссектрисе этого угла. Точка $P$ лежит на одной прямой с центрами окружности, значит, $RP$ - биссектриса треугольника $ARP.$
По теореме о биссектрисе угла треугольника $\displaystyle \frac{AP}{DP}=\displaystyle \frac{AR}{DR}=\sin \angle D.$
б) Введем обозначения. Пусть окружность с центром $O_{1}$ и радиусом $\displaystyle \frac{4}{3}$ касается сторон $AB$ и $AD$ в точках $E$ и $M,$ а окружность в цетре $O_{2}$ и радиусом $\displaystyle \frac{1}{3}$ касается сторон $AB$ и $BC$ в точках $F$ и $N.$ Проведем перпендикуляр $O_{2}H$ к отрезку $O_{1}E.$ Так как радиус, проведенный в точку касания, перпендикулярен касательной, то $HO_{2}FE$ - прямоугольник, а $AEO_{1}M$ и $BNO_{2}F$ - квадраты. Получим:
$O_{1}H=O_{1}E-HE=O_{1}E-O_{2}F=\displaystyle \frac{4}{3}-\displaystyle \frac{1}{3}=1,$
$O_{1}O_{2}=\displaystyle \frac{4}{3}+\displaystyle \frac{1}{3}=\displaystyle \frac{5}{3}.$
По теореме Пифагора из трегугольника $O_{1}O_{2}H:$
$O_{2}H=\sqrt{O_{1}O_{2}^{2}-O_{1}H^{2}}=\sqrt{\displaystyle \frac{25}{9}-1}=\displaystyle \frac{4}{3}=EF.$
Прямые $O_{2}H$ и $EF$ параллельны, значит треугольники $O_{1}O_{2}H$ и $O_{1}RE$ подобны по признаку подобия по двум углам ($\angle REO_{1}=\angle O_{2}HO_{1}=90^{\circ },$ $\angle RO_{1}E$ - общий). Тогда обозначим $\angle O_{1}O_{2}H=\angle O_{1}RE=\alpha .$
Из прямоугольного треугольника $O_{1}O_{2}H:$
$tg \alpha =\displaystyle \frac{O_{1}H}{O_{2}H}=\displaystyle \frac{3}{4}.$
Тогда $\angle BRC=2\alpha ,$ $\angle BCD=\angle CRB+\angle RBC=90^{\circ }+2\alpha $ как внешний угол треугольника и $\angle O_{2}CN=\displaystyle \frac{1}{2}\angle BCD=45^{\circ }+2\alpha $ так как центр вписанной в угол окружности лежит на биссектрисе этого угла.
Из треугольника $O_{2}CN$ находим:
$NC=O_{2}N\cdot ctg(45^{\circ }+\alpha )=O_{2}N\cdot tg(90^{\circ}-(45^{\circ }-\alpha ))=O_{2}N\cdot tg(45^{\circ }-\alpha )=$
$=\displaystyle \frac{1}{3}\cdot \displaystyle \frac{1-tg\alpha }{1+tg\alpha }=\displaystyle \frac{1}{3}\cdot \displaystyle \frac{1-\displaystyle \frac{3}{4}}{1+\displaystyle \frac{3}{4}}=\displaystyle \frac{1}{21}.$
Значит, $BC=BN+NC=\displaystyle \frac{1}{3}+\displaystyle \frac{1}{21}=\displaystyle \frac{8}{21}.$
Аналоично, $\angle O_{1}DM=tg(45^{\circ }-\alpha )$ и
$MD=O_{1}M\cdot ctg(45^{\circ }-\alpha )=O_{1}M\cdot tg(45^{\circ }-\alpha )=\displaystyle \frac{1}{4}\cdot \displaystyle \frac{1+tg\alpha }{1-tg\alpha }=\displaystyle \frac{4}{3}\cdot \displaystyle \frac{1+\displaystyle \frac{3}{4}}{1-\displaystyle \frac{3}{4}}=\displaystyle \frac{28}{3}.$
$AD=AM+MD=\displaystyle \frac{4}{3}+\displaystyle \frac{28}{3}=\displaystyle \frac{32}{3}.$
Так как $AB=AE+EF+FB=\displaystyle \frac{4}{3}+\displaystyle \frac{4}{3}+\displaystyle \frac{1}{3}=3,$ то $S_{ABCD}=\displaystyle \frac{AD+BC}{2}\cdot AB=\displaystyle \frac{\displaystyle \frac{32}{3}+\displaystyle \frac{8}{21}}{2}\cdot 3=\displaystyle \frac{116}{7}.$
Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M, а окружность с диаметром CD пересекает основание AD в точке N. Отрезки AM и CN пересекаются в точке P.
а) Докажите, что в четырёхугольник ABCP можно вписать окружность.
б) Найдите радиус этой окружности, если BC = 7, AD = 23.
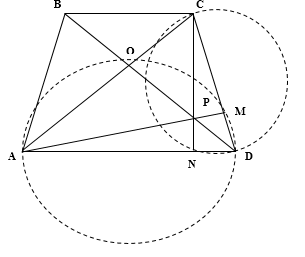
а) Пусть $O$ - точка пересечения диагоналей трапеции. Так как $AD$ и $CD$ - диаметры окружностей, то $\angle AMD=\angle CND=90^{\circ }.$ По условию $AC\perp BD\Rightarrow AC\perp BO,$ следовательно , $CN,$ $AM$ и $DO$ - высоты треугольноки $ACD.$ Они пересекаются в одной точке $P.$
Трапеция равнобедренная, а ее диагонали перпендикулярны, поэтому треугольник $BOC$ и $AOD$ - равнобедренные и прямоугольные, следовательно, $\angle CBD=\angle CAD=45^{\circ }.$ Так как $AD\perp CN,$ то $BC\perp CN.$ Значит, в прямоугольных треугольниках $BCP$ и $CAN$ углы при основании равны $45^{\circ }$ и треугольники являются равнобедренными, поэтому $BC=CP$ и $AN=CN.$
Прямая $CO$ является серединным перпендикуляром к отрезку $BD$. Точка $A$ принадлежит этой прямой, поэтому $AB=AP.$
Тогда верно, что $BC+AP=AB+CP$ (то есть суммы противоположных сторон равны), следовательно, в четырехугольнике $ABCP$ можно вписать окружностью.
б) Так как $N$ - основание высоты в равнобедренной трапеции, то
$DN=\displaystyle \frac{AD-BC}{2}=\displaystyle \frac{23-7}{2}=8,$
$CN=AN=AD-DN=23-8=15.$
По теореме Пифагора из треугольника $ACN$ $AC=\sqrt{CN^{2}+AN^{2}}=23\sqrt{2}.$
Аналогично из треугольника $BCP$ $BP=7\sqrt{2},$ из треугольника $CND$
$AB=CD=\sqrt{CN^{2}+DN^{2}}=\sqrt{225+64}=17.$
Выразим площадь четырехугольника $ABCP$ двумя способами:
$S_{ABCP}=\displaystyle \frac{1}{2}AC\cdot BP\cdot \sin 90^{\circ }=\displaystyle \frac{1}{2}P_{ABCP}\cdot r,$
$r=\displaystyle \frac{AC\cdot BP}{2(AB\cdot BC)}=\displaystyle \frac{15\sqrt{2}\cdot 7\sqrt{2}}{2\cdot 24}=4,375$
Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC = CD.
а) Докажите, что $\displaystyle \frac{AB}{BC}=\displaystyle \frac{AP}{PD}$.
б) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 5, а BC = 5√2.
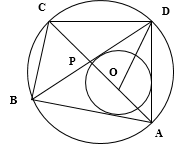
а) Вписанные углы $BAC$ и $DAC$ равны, как опирающиеся на равные хорды, значит, $AC$ - биссектриса угла $BAD. $
Вписанные углы $ADB$ и $ACB$ опираются на одну и ту же дугу, поэтому они тоже равны. Значит, треугольники $ADP$ и $ACB$ подобные по двум углам. Следовательно, $\displaystyle \frac{AB}{BC}=\displaystyle \frac{AP}{PD}.$
б) Точки $A$ и $C$ принадлежит окружности с диаметром $BD$, значит, треугольники $ABD$ и $BCD$ прямоугольные. По условию треугольник $BCD$ равнобедренный, поэтому $BD=BC\sqrt{2}=10$ и углы при основании равны $45^{\circ }.$
Катет $AB$ прямоугольного треугольника $ABD$ равен половине гипотенузы $BD,$ следовательно, $\angle ADB=30^{\circ },\angle ABD=60^{\circ }.$
Так ка центр окружности, вписанной в треугольник, - точка пересечения его биссектрис, то точка $O$ лежит на биссектрисе $AC$ угла $BAD$ и на биссектрисе угла $ADB.$ Тогда $\angle ACD=\angle ABD=60^{\circ }$ (как опирающиеся на одну хорду) и $\angle ODB=\displaystyle \frac{1}{2}\angle ADB=15^{\circ }. $ Получаем, что $\angle ODC=\angle ODB+\angle BDC=15^{\circ }+45^{\circ }=60^{\circ }.$
Значит, треугольник $COD$ - равностронний со стороной $5\sqrt{2}.$
$S_{COD}=\displaystyle \frac{CD^{2}\sqrt{3}}{4}=\displaystyle \frac{25\sqrt{3}}{2}.$
В ответе необходимо записать полученное значение пункта б), умноженное на √3, то есть 37,5.

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

Решено верно

«Выбери тест, предмет и нажми кнопку «Начать решать»

После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию

Решай задания и записывай ответы. После 1-ой попытки ты сможешь посмотреть решение

Сбоку ты можешь посмотреть статистику и прогресс по предмету

Нажми, чтобы начать решать вариант. Как только ты перейдешь на страницу, запустится счетчик времени, поэтому подготовь заранее все, что может тебе понадобиться

Отмечай те статьи, что прочитал, чтобы было удобнее ориентироваться в оглавлении

Ты прошел обучение! Теперь ты знаешь как пользоваться сайтом и можешь переходить к решению заданий