

17. Механика
 Читать 0 мин.
Читать 0 мин.
17.508. Гравитация
равитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m1 и m2, разделёнными расстоянием r, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть:
F = $G\frac{m_1m_2}{R^2}$ , где
F ― сила гравитации [Н],
m1 и m2 ― массы тел [кг],
R ― расстояние между телами [м],
G — гравитационная постоянная, равная 6,7 ∙ 10−11 [Нм2/кг2].
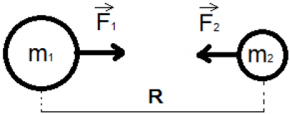
По 3ему закону Ньютона F1 = F2.
Ускорения свободного падения для всех тел одинаково и не зависит от массы тела. Тяжелое и легкое тело в отсутствии силы сопротивления воздуха будут падать вниз с одинаковой скоростью.
Первая космическая скорость — скорость, необходимая для движения по орбите планеты. Получим формулу для этой величины: под действием гравитационной силы тело совершает движение по окружности, поэтому запишем второй закон Ньютона:
$G\frac{mM}{R^2} = ma$ , где m ― масса тела, а М ― масса планеты.
Учтя, что при движении по окружности тело обладает нормальным ускорением, запишем $G\frac{mM}{R^2} = m\frac{V^2}{R}$ , сократив массы и радиус, выразим скорость $V = \sqrt{G\frac{M}{R}}$ .
Так, первая космическая скорость выражается формулой:
$V = \sqrt{G\frac{M}{R}}$ , где
V ― первая космическая скорость $\big[ \frac{\text{м}}{c} \big]$ ,
М ― масса планеты [кг],
G — гравитационная постоянная, равная 6,7 ∙ 10−11 [Нм2/кг2],
R ― радиус орбиты [м].






















