

35. Электродинамика
 Читать 0 мин.
Читать 0 мин.
35.40. Электростатика
Кулону экспериментально удалось установить закон взаимодействия неподвижных заряженных тел ― закон Кулона: сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.
F = $k\frac{q_1q_2}{r^2}$ , где
F ― сила Кулона [Н];
q1, q2 ― заряды [Кл];
r ― расстояние между зарядами [м];
k ― коэффициент пропорциональности равный 9 ∙ 109 $\big[ \frac{H \cdot \text{м}^2}{\text{Кл}^2} \big]$ .
При этом оказалось, что заряды одного знака отталкиваются, а заряды разных знаков притягиваются.
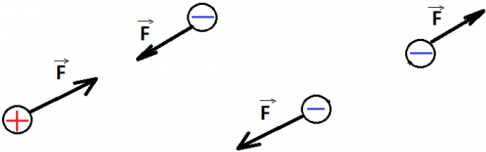
Напряженностью электрического поля называется векторная физическая величина, равная отношению силы, с которой поле действует на пробный точечный заряд, к величине этого заряда.
$\overrightarrow{E} = \frac{\overrightarrow{F}}{q}$
Напряженность электрического поля «выходит» из положительного заряда и «входит» в отрицательный.
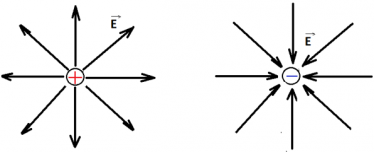
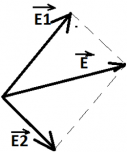
Принцип суперпозиции полей: если в точке пространства несколько заряженных частиц создают поля, напряженности которых равны $\overrightarrow{E_1}, \overrightarrow{E_2}$ , то результирующая напряженность поля в этой точке равна векторной сумме полей $\overrightarrow{E} = \overrightarrow{E_1} + \overrightarrow{E_2}$ .
Разность потенциалов между двумя точками в постоянном электрическом поле определяется выражением ∆φ = –Ed
∆φ ― разность потенциалов [В];
E ― напряженность однородного электрического поля [В/м];
d ― расстояние между точками, между которыми определяется разность потенциалов. [м].
Работа совершаемая электрическими силами определяется через разность потенциалов, как A = –∆φq:
А ― работа [Дж];
∆φ ― разность потенциалов [В];
q ― заряд [Кл].
Работа не зависит от траектории, а зависит только от начального и конечного положения тела.
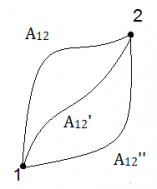
$A_{12} = A_{12'} = A_{1'2'}$
Для потенциала так же справедлив принцип суперпозиции: потенциал поля, созданного в точке несколькими точечными зарядами, равен сумме потенциалов полей, создаваемых в этой точке каждым зарядом по отдельности:
φ = φ1 + φ2 + φ3 + …






















