Импульс тела: $\overrightarrow{p} = m\cdot \overrightarrow{v}$ , где $\overrightarrow{p}$ ― импульс тела (кг∙м/с), m ― масса тела (кг), $\overrightarrow{v}$ ― скорость тела (м/с).

Импульс ― векторная величина и сонаправлена со скоростью тела.

Тела могут обмениваться импульсами. Например, если движущийся шарик столкнется с покоящимся, то дальше они оба приобретут скорость и начнут двигаться. Для того, чтобы понять, как передается импульс и вычислить его, возникла необходимость распознавать разные виды ударов.

Удар, после которого объекты продолжают существовать отдельно ― абсолютно упругий удар.

Удар, после которого тела слипаются и двигаются вместе ― абсолютно неупругий.

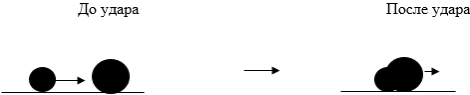
Возникает вопрос: зачем вообще нужен этот импульс? На самом деле импульс ― это еще одна величина, которая, как и энергия сохраняется. Как и для энергии, для импульса существует закон сохранения и формулируется он очень похоже: в замкнутой системе векторная сумма импульсов всех тел системы постоянна. Именно свойство сохранения импульса делает его такой важной для нас величиной.

$\overrightarrow{p_1} + \overrightarrow{p_2} = \overrightarrow{p_1}' + \overrightarrow{p_2}'$ 

Закон сохранения импульса для разных ударов:

для абсолютно упругого удара: $m_1 \overrightarrow{v_1} + m_2 \overrightarrow{v_2} = m_1 \overrightarrow{u_1} + m_2\overrightarrow{u_2} $

для абсолютно неупругого удара: $m \overrightarrow{v_1} + m_2 \overrightarrow{v_2} = (m_1+m_2) \overrightarrow{u}$

Если при отсутствии внешних сил импульс сохраняется, то, когда появятся внешне силы он начнет изменяться. Причем важно не только значение воздействующей силы, но и время ее воздействия:

$\Delta\overrightarrow{p} = \overrightarrow{F}\Delta t $ , где $\Delta\overrightarrow{p}$ ― изменение импульса (кг·м/с), $\overrightarrow{F}$ ― сила (Н), ∆t ― время (с).