

42. Электродинамика
 Читать 0 мин.
Читать 0 мин.
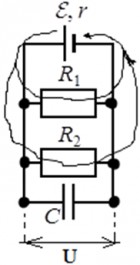
42.430. Цепи
Через конденсатор постоянный ток не течёт.
Напряжение на параллельных участках цепи одинаково.
В системе отключенных конденсаторов заряд всегда остаётся постоянным. Напряжение и ёмкость может меняться.
Выделившееся количество теплоты равно разности начальной и конечной энергии:
Q = Eн – Ек ¸ где
Q ― выделившееся тепло [Дж];
Eн ― начальная энергия системы [Дж];
Ек ― конечная энергия системы [Дж].
Начальные и конечные энергии определяются энергиями конденсаторов и катушек индуктивности входящих в цепь.
После установления равновесия, напряжение есть только на конденсаторах, не подключенных параллельно к резисторам.
Конденсатор в цепи постоянного тока
Плоский конденсатор представляет собой пластинки, на которых может скапливаться заряд. Между пластинками находится пространство, заполненное диэлектриком (или воздухом в роли диэлектрика). Поскольку диэлектрики ― вещества, плохо проводящие ток, от одной пластины конденсатора через слой диэлектрика на другую пластину заряд перейти не может, а значит, через конденсатор ток не проходит. Если на участке цепи находится такой конденсатор ― этот участок «заблокирован», тока в нем нет.
Если на участке цепи находится конденсатор не заряженный, или заряженный частично, а цепь подключают к источнику тока ― на обкладках конденсатора начинает скапливаться заряд. Это означает, что на этом участке цепи до конденсатора есть ток ― до тех пор, пока конденсатор не заряжен полностью.
Если цепь от источника тока отключить, и в ней есть заряженный конденсатор ― конденсатор начинает разряжаться. Заряды с одной обкладки конденсатора пытаются перейти на другую, по «длинному пути» ― через всю цепь, создавая, таким образом, ток. Ток в такой цепи будет до тех пор, пока конденсатор не разрядится.
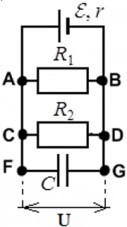
Пример: Пусть в цепи есть два резистора с сопротивлениями R1 и R2, источник ЭДС ε, и конденсатор емкостью C:
Конденсатор C полностью заряжен. В этом случае токи в цепи не проходят через участок цепи FG ― его словно нет в цепи, и в расчетах параметров цепи он не учитывается. Ток считается выходящим из положительно заряженной клеммы источника ЭДС (тонкая и длинная) к входящим в отрицательно заряженную клемму (жирная короткая черта):
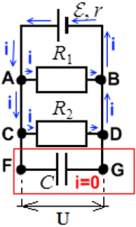
Конденсатор разряжен или заряжен не док конца. В этом случае конденсатор только заряжается, и ток в цепи через точку F проходит - вплоть до обкладки конденсатора – но дальше, в точку G ток не проходит.
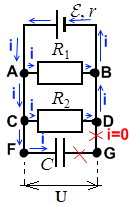
Конденсатор заряжен, но от источника ЭДС цепь отключена. В этом случае ток идет через всю цепь ― пока конденсатор может служить источником зарядов и пока полностью не разрядится. Когда конденсатор разрядится ― ток в цепи прекратится.
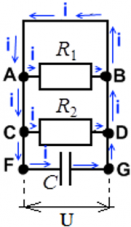
Напряжения на всех параллельных участках цепи равны ― это основное свойство параллельного подключения. Вне зависимости от того, находится на ветви резистор, или конденсатор. Таким образом, во всех случаях для примера выше, напряжение на конденсаторе C равно напряжению на резисторе R1, и равно напряжению на резисторе R2. Благодаря этому свойству, зная, например, энергию, скопившуюся на заряженном конденсаторе, или его заряд, можно вычислить напряжение на резисторах.
Заряженный конденсатор, отключенный от цепи. У заряженного конденсатора на обкладках находится определенное количество заряда. Если конденсатор отключить от цепи ― заряду некуда переместиться, и он остается на конденсаторе неизменным. Получить дополнительный заряд, если он заряжен не до конца, конденсатору тоже неоткуда. Заряд конденсатора, отключенного от цепи, постоянен.
Электроемкость конденсатора ― это его физико-геометрическая характеристика, показывающая, как много заряда он может скопить. Электроемкость конденсатор не зависит ни от заряда на его обкладках, ни от напряжения в цепи.
Электроемкость конденсатора равна C = $\frac{q}{\varphi_2 - \varphi_1} = \frac{q}{U}$ , где
C ― электроемкость конденсатора, [Ф];
q ― заряд конденсатора, [Кл];
(φ2 – φ1) ― разность потенциалов на обкладках конденсатора, [В];
U ― напряжение на обкладках конденсатора [В].
Электроемкость плоского конденсатора зависит от размеров его пластин, расстояния между ними, а также типа диэлектрика, который заполняет пространство между пластинами.
Электроемкость плоского конденсатора равна C = $\frac{\varepsilon\varepsilon_0 S}{d}$ , где
C ― ёмкость конденсатора [Ф];
ε ― диэлектрическая проницаемость;
ε0 ― электрическая постоянная;
S ― площадь обкладок конденсатора [м2];
d ― расстояние между обкладками [м].
В электрической цепи за счет сопротивления, которое преодолевают движущиеся в материале заряды, выделяется тепло. Количество теплоты, которая выделяется в цепи, равно разности начальной и конечной энергии всей системы Q = Eн – Eк¸ где
Q ― выделившееся тепло [Дж];
Eн ― начальная энергия системы [Дж];
Eк ― конечная энергия системы [Дж].
В цепи энергия скапливается на конденсаторах (энергия электрического поля) и на катушках индуктивности (энергия магнитного поля). Поэтому энергия электромагнитных сил в цепи в любой момент равна сумме энергий на конденсаторах и на катушках, которые входят в цепь.
Энергия электрического поля заряженного конденсатора равна We = $\frac{CU^2}{2} = \frac{qU}{2} = \frac{q^2}{2C}$ , где
We ― энергия электрического поля конденсатора, [Дж];
C ― электроемкость конденсатора, [Ф];
U ― напряжение на обкладках конденсатора, [В];
q ― заряд на обкладках конденсатора, [Кл].
Энергия магнитного поля катушки индуктивности равна E = $\frac{LI^2}{2}$ , где
E ― энергия магнитного поля катушки [Дж];
L ― индуктивность катушки [Гн];
I ― сила тока в катушке [А].
Состояние равновесия и зарядка конденсаторов
Пример 1: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, оба конденсатора емкостями C1 и C2 разряжены.
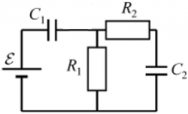
Ток от источника ЭДС до конденсатора C1 будет идти до тех пор, пока конденсатор C1 не будет полностью заряжен. При этом от конденсатора C1 дальше заряды не проходят ― ни на резисторы R1 и R2, ни на конденсаторC2. Как только конденсатор C1 полностью заряжается, в системе наступает состояние равновесия ― напряжение на конденсаторе становится равным ЭДС, весь возможный заряд конденсатор принял. Поскольку ток через него не прошел до конденсатора C2 ― этот конденсатор так и остался незаряженным. Напряжение есть лишь на конденсаторе C1, а на конденсаторе C2напряжение равно нулю. Зарядка конденсатораC1:
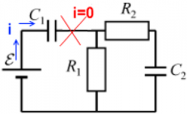
После того, как конденсатор C1 заряжен, ток в цепи прекращается.
Пример 2: в цепи, изображенной на рисунке, есть ЭДС и резисторы с сопротивлениями R1 и R2, все три конденсатора емкостями C1, C2 и C3 разряжены.
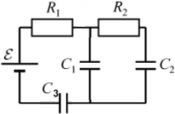
Ток, выходя из источника ЭДС, разделяется на два тока ― один питает подзарядку конденсатораC1, а другой ― конденсатораC2. Состояние равновесия наступает, когда оба конденсатора полностью заряжены ― в цепи ток больше не проходит. Но так как ток дальше конденсаторов не проходит ― конденсатор C3 не получает заряд, и остается разряженным. Напряжение на конденсаторе C3 равно нулю.
Зарядка конденсаторов C1 иC2:
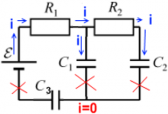
После того, как конденсаторыC1 и C2 заряжены, ток в цепи прекращается.






















