Любое космическое тело для удобства расчетов можно считать шаром, плотность которого одинакова в любой точке и равна некоторому среднему значению плотностей всех отдельных точек. В таком случае формула эквивалентности массы, плотности и объема с учетом геометрической формул объема шара будет иметь вид:

Связь массы, плотности и радиуса любого космического тела: $M = \frac{4}{3}\pi \rho R^3$

M – Масса тела [кг]

R – Примерный радиус тела [м]

ρ – Средняя плотность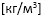 

Для удобства оценки массы двух космических тел на предмет отличий стоит заметить, что согласно формуле, масса зависит от плотности и третьей степени радиуса тела.

Также высокую применимость имеют все формулы гравитации, поэтому есть необходимость напомнить их:

Ускорение свободного падения на поверхности любого космического тела: $g = \frac{GM}{R^2}$

Первая космическая скорость вблизи поверхности любого космического тела: $V_1 = \sqrt{\frac{GM}{R}}$

G – Гравитационная постоянная, равная $6,7 \cdot 10^{-11} H \cdot \text{м}^2/\text{кг}^2 $

M – Масса тела [кг]

R – Примерный радиус тела [м]

Комбинация этих формул может дать еще одну применимую на ЕГЭ формулу:

Первая космическая скорость вблизи поверхности любого космического тела выраженная через ускорениесвободного падения на поверхности этого тела: $V_1 =\sqrt{gR}$

Для получения последней формулы необходимо внести определение эксцентриситета орбиты.

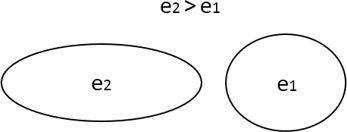
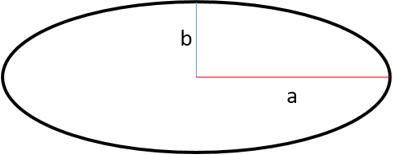
Эксцентриситет – мера отличия эллипса от окружности, существует в границах 0

Так, если сравнить два эллипса с эксцентриситетами e2 > e1, то второй эллипс будет более вытянут в горизонтальной плоскости и сильнее сжат в вертикальной.

Чем меньше значение эксцентриситета, тем сильнее орбита похожа на окружность, а чем больше – тем сильнее отличается. При эксцентриситете, равном единице, орбита тела становится параболой.

Эксцентриситет эллиптической орбиты можно найти по следующей формуле: $\varepsilon = \sqrt{1 - \frac{b^2}{a^2}}, \text{где} \; b - \text{малая полуось}, a - \text{большая полуось эллипса}$

Замкнутость орбиты вызвана попыткой тела покинуть гравитационное притяжение своего небесного тела (планеты/спутника/астероида). Если телу удается покинуть гравитационное притяжение планеты (то есть эксцентриситет тела стал равен 1), значит тело достигло второй космической скорости (скорость убегания) — наименьшей скорости, которую необходимо придать объекту для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него.

Формула второй космической скорости: $V_{11} = \sqrt{2}V_1 = \sqrt{2gR} = \sqrt{\frac{2GM}{R}}$, где все величины уже были введены в формулах выше.