

31. Текстовые задачи
 Читать 0 мин.
Читать 0 мин.
31.296. Текстовые задачи на производительность
Суть задач на производительность следующая: некоторую работу выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью. Они могут выполнять эту работу либо по отдельности, либо совместно друг с другом. Алгоритм решения здесь такой же, как и алгоритм решения задач на движение:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Основные особенности решения задач на производительность:
- Задачи на производительность схожи с задачами на движение. Основная формула при решении: V = v·t. Сравните её с формулой для решения задач на движение S = v·t. Роль скорости v здесь играет производительность труда, а роль расстояния S — объем работы V.
- Объем работы может быть не дан по условию и его не нужно находить при решении задачи (нам просто напросто не важно, какой объем работы выполняется). В таком случае его можно обозначить какой-нибудь буквой, например, V или A. В процессе решения эта переменная, которой мы обозначили объем, сократится и её значение не придется находить.
- Также, если объем работы не дан по условию, удобно принять его просто за 1; тогда время t, требующееся для выполнения всей работы, иv – производительность труда, связаны формулой:
$ \ t=\frac{1}{\upsilon}. $
- В отличие от задач на движение, в задачах на производительность скорости выполнения работы не могут вычитаться, а могут только складываться друг с другом. Если два человека или механизма по отдельности работают с производительностями v1 и v2, то вместе они будут работать быстрее (никак не медленнее), с суммарной производительностью v1 + v2, а время совместной работы будет равно:
$ \ t=\frac{1}{\upsilon_{1}+\upsilon_{2}} $
Пример:
Первый рабочий за час делает на 5 деталей больше, чем второй, и выполняет заказ, состоящий из 200 деталей, на 2 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Решение:
В задаче требуется найти производительность второго рабочего. Примем его скорость за x. Заполним таблицу.
| v, дет/ч | t, ч | V, дет | |
|---|---|---|---|
|
Первый рабочий |
x + 5 |
$ \frac{200}{x+5} $ |
200 |
|
Второй рабочий |
x |
$ \frac{200}{x} $ |
200 |
В условии задачи сказано, что первый рабочий выполняет заказ на 2 часа быстрее, чем второй. На основании этого составим уравнение:
$ {\frac{200}{x+5}+2=\frac{200}{x} \frac{200+2x+10}{x+5}=\frac{200}{x}.} $
2x2 + 210x = 200x + 1000;
x2 + 5x – 500 = 0.
Получаем два корня, x1= 20 и x2= –25. Второй корень не подходит, так как производительность не может быть отрицательной.
Ответ: 20 дет/ч.
Виды задач на производительность:
1. Задачи на совместную работу:
Задачи на совместную работу — это тип задач, в которых объектами, выполняющими работу, являются люди или группы людей: рабочие, ученики, операторы, бригады рабочих и т п. Объекты могут выполнять работу по отдельности, а могут — вместе.
Разберем простой пример. Двум рабочим требуется выполнить работу. Допустим, первый рабочий выполняет всю работу за 10 часов, а второй — за 5. Давайте найдем, за сколько часов рабочие справятся с работой, выполняя её вместе.
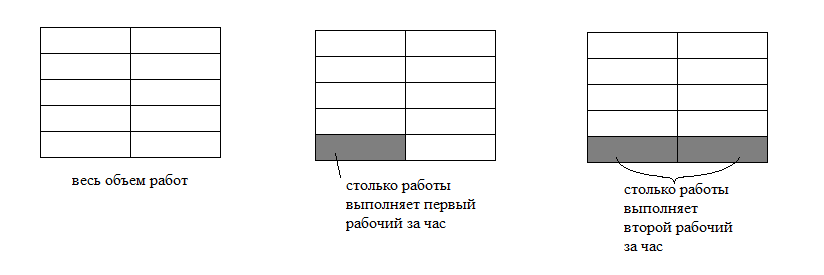
Получается, что если принять весь объем работ за 1, то первый рабочий выполняет $ \frac{1}{10} $ всей работы за час, а второй $ \frac{1}{10} $ то есть $ \frac{1}{10} $ всей работы за час. На рисунке весь объем работ — это 10 «кирпичиков», первый выполняет 1 «кирпичик» за час, а второй — 2. Тогда вместе они будут выполнять $ \frac{1}{10}+ \frac{1}{5}= \frac{3}{10} $ всей работы за час, или 3 «кирпичика»:
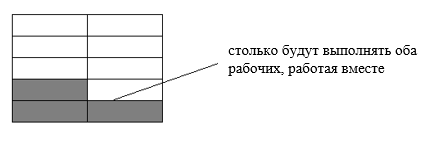
Чтобы найти совместную производительность рабочих, мы сложили друг с другом их собственные производительности. Теперь, чтобы найти время, за которое оба рабочих справятся с работой, выполняя её вместе, разделим полный объем работ на совместную производительность:
$ 1/\frac{3}{10}=\frac{10}{3}=3\frac{1}{3} $
То есть вместе рабочие справятся с работой за 3 $ \frac{1}{3} $ часа, или за 3 часа 20 минут.
2. Задачи на бассейны и трубы:
Отдельно можно выделить группу задач на производительность — задачи на заполнение бассейна несколькими трубами. В таких задачах рабочим будут соответствовать насосы (или трубы) разной производительности, а объему работы — объем бассейна или иного резервуара.
Рассмотрим пример. Две трубы наполняют бассейн за 6 часов, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?
Получается, что за 1 час две трубы наполняют $ \frac{1}{6} $ часть бассейна, а одна первая труба наполняет $ \frac{1}{9} $ часть бассейна: Так как вместе трубы наполняют бассейн водой со скоростью, равной сумме скоростей отдельно каждой из труб, то вторая труба наполняет бассейн со скоростью $ \frac{1}{6}- \frac{1}{9}= \frac{1}{18} $.
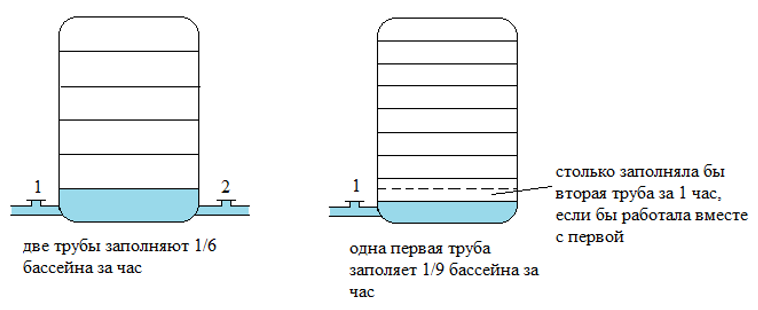
Таким образом, вторая труба заполнит бассейн за $ 1/\frac{1}{18}=18 $ часов.






















