55. Планиметрия
 Читать 0 мин.
Читать 0 мин.
55.360. Трапеция
Трапеция ― это четырёхугольник, у которого две противоположные стороны параллельны и ОБЯЗАТЕЛЬНО не равны (потому что в этом случае эта фигура будет является параллелограммом).
Элементы трапеции:
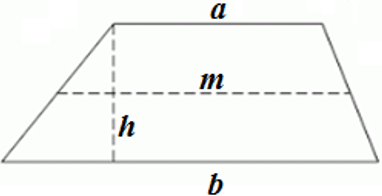
a и b ― основания трапеции, a || b;
h ― высота трапеции (расстояние между основаниями);
m ― средняя линия трапеции (отрезок, соединяющий середины боковых сторон трапеции).
Средняя линия трапеции равна полусумме оснований: $m = \frac{a + b}{2}$ и параллельна им: m || a и m || b.
Виды трапеций:
1) Прямоугольная ― трапеция, имеющая прямые углы при боковой стороне:
- боковая сторона является высотой.

2) Равнобедренная ― трапеция, у которой боковые стороны равны:
- углы при основаниях равны
- длины диагоналей равны

3) Произвольная ― не является ни прямоугольной, ни равнобедренной.
Свойства трапеции:
- Сумма внутренних углов трапеции (как и любого четырехугольника) равна 360°.
- Сумма углов, прилежащих к боковой стороне, равна 180°.
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
- Если трапецию можно вписать в окружность, то трапеция ― равнобедренная.
- Около равнобедренной трапеции можно описать окружность.
- Треугольники BOC и AOD подобны по двум углам. (∠1=∠2, ∠3=∠4 – как накрест лежащие).

Площадь трапеции:
|
1 |
2 |
3 |
|
|
|
|
|
$S = \frac{a + b}{2}\cdot h$ |
S = m ∙ h, где m ― средняя линия трапеции. |
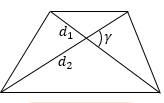
$S = \frac{1}{2}d_1d_2\sin \gamma$ |
|
Площадь трапеции равна произведению полусуммы оснований на высоту. |
Площадь трапеции равна произведению средней линии на высоту. |
Площадь трапеции равна половине произведения диагоналей синус угла между ними. |