40. Алгебра
 Читать 0 мин.
Читать 0 мин.
40.572. Формулы тригонометрии
Основные тригонометрические формулы
| $ sin^{2}\alpha + cos^{2} \alpha = 1 $ |
| $ tg \alpha = \frac {sin \alpha}{cos \alpha}, \; \alpha \neq \frac {\pi} {2}+\pi n, \; n \in Z $ |
| $ ctg \alpha = \frac {cos \alpha}{sin \alpha}, \; \alpha \neq \pi n, \; n \in Z $ |
| $ tg \alpha \cdot ctg \alpha = 1, \; \alpha \neq \frac {\pi n} {2}, \; n \in Z $ |
| $ 1+tg^{2} \alpha = \frac{1}{cos^{2} \alpha}, \; \alpha \neq \frac {\pi}{2}+ \pi n, \; n \in Z $ |
| $ 1+ctg^{2} \alpha = \frac{1}{sin^{2} \alpha}, \; \alpha \neq \pi n, \; n \in Z $ |
Пример. Найти значение выражения:
$ 5sin^{2}5x+5cos^{2}5x $
Решение. Применяем основное тригонометрическое тождество в виде:
$ sin^{2}5x+cos^{2}5x=1 $
$ 5sin^{2}5x+5cos^{2}5x=5(sin^{2}5x+cos^{2}5x)=5 \cdot 1=5 $
Пример. Найти значение выражения:
$ \frac {cos^{2}x}{1+tg^{2}x} $ при $ cos x = \frac {1}{\sqrt 2} $
Решение. Из основного тригонометрического тождества $ sin^{2}x+cos^{2}x=1 $ следует:
$ tg^{2}x+1= \frac {1}{cos^{2}x} $
Подставим в выражение:
$ \frac {cos^{2}x}{1+tg^{2}x}=\frac {cos^{2}x}{\frac {1}{cos^{2}x}}=cos^{4}x= \big(\frac {1}{\sqrt 2} \big)^{4}= \frac {1}{4}=0,25 $
Тригонометрические формулы суммы и разности двух углов
| Формула | Название формулы |
| $ sin(\alpha+\beta)=sin \alpha \cdot cos \beta+cos \alpha \cdot sin \beta $ | Синус суммы |
| $ sin(\alpha-\beta)=sin \alpha \cdot cos \beta-cos \alpha \cdot sin \beta $ | Синус разности |
| $ cos(\alpha+\beta)=cos \alpha \cdot cos \beta-sin \alpha \cdot sin \beta $ | Косинус суммы |
| $ cos(\alpha-\beta)=cos \alpha \cdot cos \beta+sin \alpha \cdot sin \beta $ | Косинус разности |
| $ tg(\alpha+\beta)= \frac {tg \alpha+tg \beta}{1-tg \alpha \cdot tg \beta} \\ \alpha, \; \beta, \; \alpha + \beta \neq \frac {\pi}{2} + \pi n, \; n \in Z$ | Тангенс суммы |
| $ tg(\alpha-\beta)= \frac {tg \alpha-tg \beta}{1+tg \alpha \cdot tg \beta} \\ \alpha, \; \beta, \; \alpha + \beta \neq \frac {\pi}{2} + \pi n, \; n \in Z$ | Тангенс разности |
Пример. Вычислить $ \sqrt 2 (1 - \sqrt 3) sin 105^{\circ} $
Решение. $ sin 105^{\circ}=sin(60^{\circ}+45^{\circ})=sin 60 ^{\circ} \cdot cos 45 ^{\circ} + cos 60 ^{\circ} \cdot sin 45 ^{\circ} = \frac {\sqrt 3}{2} \cdot \frac {\sqrt 2}{2}+\frac {1}{2}\cdot \frac {\sqrt 2}{2}=\frac {\sqrt 2}{4}(1+\sqrt 3) $.
$ \sqrt 2(1-\sqrt 3) sin 105^{\circ}=\sqrt 2(1-\sqrt 3)\frac {\sqrt 2}{4}(1+\sqrt 3)=\frac {1}{2} (1^{2}- \sqrt 3^{2})=0,5 \cdot (-2)=-1 $
Пример. Вычислить $ \sqrt 2 (1- \sqrt 3) cos \frac {13 \pi}{12} $.
Решение. $ cos \frac {13 \pi}{12}=cos \big(\frac {3 \pi}{4} + \frac {\pi}{3} \big)=cos \frac {3 \pi}{4} \cdot cos \frac {\pi}{3} - sin \frac {3 \pi}{4} \cdot cos \frac {\pi}{3} = - \frac {\sqrt 2}{2} \cdot \frac {1}{2} - \frac {\sqrt 2}{2} \cdot \frac {\sqrt 3}{2} = -\frac {\sqrt 2}{4} (1+\sqrt 3) $.
$ \sqrt 2(1-\sqrt 3) cos \frac {13 \pi}{12}= \sqrt 2(1-\sqrt 3)( -\frac {\sqrt 2}{4}(1+\sqrt 3)=- \frac {1} {2}(1^{2}- \sqrt 3^{2} )=-0,5 \cdot (-2)=1 $
Тригонометрические формулы двойного угла
| Формула | Название формулы |
| $ sin2 \alpha=2sin\alpha \cdot cos \alpha $ | Синус двойного угла |
| $ cos2 \alpha = cos ^{2} \alpha - sin ^{2} \alpha \\ cos2 \alpha = 2cos^{2} \alpha - 1 \\ cos2 \alpha = 1 - 2sin^{2} \alpha $ | Косинус двойного угла |
| $ tg2 \alpha = \frac {2tg \alpha}{1-tg^{2} \alpha} \\ \alpha \neq \frac {\pi}{4}+ \frac{\pi n}{2}, \; n \in Z$ | Тангенс двойного угла |
Пример. Найдите 2cos2α, если sinα = - 0,7.
Решение. Используем формулу косинуса двойного угла: cos2α = 1 – 2sin²α.
Получаем: 2cos2α = 2·(1 – 2sin²α) = 2·(1-2·(-0,7)2) = 2·(1-2·0,49) = 0,04.
Пример. Найдите значение выражения $ \frac {12 sin 11^{\circ} \cdot cos 11^{\circ}}{sin 22^{\circ}} $
Решение. Применяем формулу sin2α = 2sinα·cosα:
$ \frac {12 sin 11^{\circ} \cdot cos 11^{\circ}}{sin 22^{\circ}} = \frac {6 sin 22^{\circ}}{sin 22^{\circ}} = 6 $.
Формулы понижения степени
| Формула | Название формулы |
| $ sin^{2} \alpha = \frac {1 - cos 2 \alpha}{2} $ | ражение квадратного синуса через косинус двойного угла |
| $ cos^{2} \alpha = \frac {1 + cos 2 \alpha}{2} $ | Выражение квадратного косинусачерез косинус двойного угла |
| $ tg^{2} \alpha = \frac {1 - cos 2 \alpha}{1 + cos 2 \alpha} \\ \alpha \neq \frac {\pi}{2}+ \pi n, \; n \in Z$ | Выражение квадрата тангенсачерез косинус двойного угла |
Пример. Найти значение выражения $ 3sin^{2}4x $, если $ cos8x=0,5 $
Решение. Используем формулу понижения степени:
$ sin^{2}x= \frac {1-cos2x}{2} $
Применительно к углам 4x и 8x она будет выглядеть так:
$ sin^{2}4x= \frac {1-cos8x}{2} $
Находим значение выражения:
$ 3sin^{2}4x= 3 \cdot \frac {1-cos8x}{2}= 3 \cdot \frac {1-0,5}{2}= 3 \cdot \frac {3 \cdot 0,5}{2}= \frac {3}{4}=0,75 $
Тригонометрические формулы произведения
| Формула | Название формулы |
| $ sin \alpha \cdot sin \beta = \frac {1}{2} (cos (\alpha-\beta)-cos(\alpha+\beta)) $ | Произведение синусов |
| $ cos \alpha \cdot cos \beta = \frac {1}{2} (cos (\alpha-\beta)-cos(\alpha+\beta)) $ | Произведение косинусов |
| $ sin \alpha \cdot cos \beta = \frac {1}{2} (sin (\alpha+\beta)+sin(\alpha-\beta)) $ | Произведение синуса и косинуса |
Пример. Вычислить sin 20°·sin 40°, считать, что cos 20° = 0,9
Решение. Заметим, что
$ sin 20 ^ {\circ} \cdot sin 40 ^{\circ} = \frac {1}{2}(cos (20^{\circ}-40^{\circ}) - cos (20^{\circ}+40^{\circ}))=\frac {1}{2}(cos20^{\circ}-cos60^{\circ})=0,5 \cdot(0,9-0,5)=0,2 $.
Формулы суммы и разности тригонометрических функций
$ sin \alpha + sin \beta = 2sin^{\frac {\alpha + \beta}{2}} \cdot cos ^{\frac {\alpha-\beta}{2}}; \\ sin \alpha - sin \beta = 2sin ^{\frac {\alpha - \beta}{2}} \cdot cos ^{\frac {\alpha+\beta}{2}}; \\ cos \alpha + cos \beta = 2cos ^{\frac {\alpha + \beta}{2}} \cdot cos ^{\frac {\alpha-\beta}{2}}; \\ cos \alpha - cos \beta = -2sin ^{\frac {\alpha + \beta}{2}} \cdot sin ^{\frac {\alpha-\beta}{2}}. $
Формулы приведения
Формул приведения много, а точнее 32. И все формулы надо знать. К счастью существует простое мнемоническое правило, позволяющее быстро воспроизвести любую формулу приведения.
Каждая формула связывает между собой либо синус с косинусом, либо тангенс с котангенсом. Причём, первая функция либо меняется на вторую, либо нет.
1. В левой части формулы аргумент представляет собой сумму или разность одного из «основных координатных углов»: $ \frac {\pi}{2}, \pi, \frac {3\pi}{2}, 2\pi $ и острого угла $ \alpha $, а в правой части аргумент $ \alpha $
2. В правой части знак перед функцией либо «плюс», либо «минус».
Мнемоническое правило
Достаточно задать себе два вопроса:
1. Меняется ли функция на кофункцию?
Ответ: Если в формуле присутствуют углы $ \frac {\pi}{2} $ или $ \frac {3\pi}{2} $ — это углы вертикальной оси, киваем головой по вертикали и сами себе отвечаем: «Да», если же присутствуют углы горизонтальной оси π или 2π, то киваем головой по горизонтали и получаем ответ: «Нет».
2. Какой знак надо поставить в правой части формулы?
Ответ: Знак определяем по левой части. Смотрим, в какую четверть попадает угол, и вспоминаем, какой знак в этой четверти имеет функция, стоящая в левой части.
Например, sin $ ( \frac {3 \pi}{2} + \alpha ) $.
1) «Меняется функция или нет?»
$ \frac {3\pi}{2} $ — угол вертикальной оси, киваем головой по вертикали: «Да, меняется». Значит, в правой части будет cosα.
2) «Знак?»
Угол $ ( \frac {3 \pi}{2} + \alpha ) $ попадает в IV четверть. Синус в IV четверти имеет знак «минус». Значит, в правой части ставим знак «минус».
Итак, получили формулу, sin $ ( \frac {3 \pi}{2} + \alpha ) = –cosα. $
Пример. Найдите значение выражения $ \frac {14sin409^{\circ}}{sin49^{\circ}} $
Решение. Используем формулу приведения:
$ \frac {14sin409^{\circ}}{sin49^{\circ}} = \frac {14sin(360^{\circ}+49^{\circ})}{sin49^{\circ}}=\frac {14sin49^{\circ}}{sin49^{\circ}}=\frac {14}{1}=14 $
Пример. Найдите значение выражения $ 5tg17^{\circ} · tg107^{\circ} $.
Решение. Используем формулу приведения:
$ 5tg17^{\circ} · tg107^{\circ} = 5tg17^{\circ}·tg(90^{\circ} + 17^{\circ}) = 5tg17^{\circ}·(−ctg17^{\circ}) = −5(tg17^{\circ}·ctg17^{\circ}) = −5·1 = −5$.
Тригонометрический круг
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Он заменяет десяток таблиц.
Сколько полезного на этом рисунке!
1. Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или 2π радиан.
2. Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси x, а значение синуса — на оси y.
3. И синус, и косинус принимают значения от –1 до 1.
Тригонометрический круг:
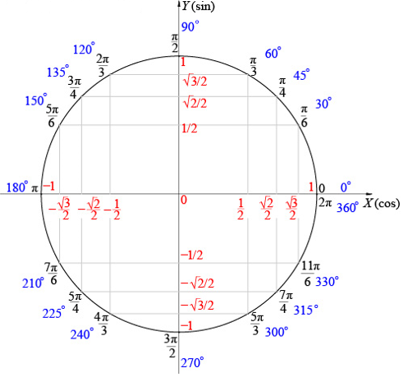
1. Значение тангенса угла α тоже легко найти — поделив sinα на cosα. А чтобы найти котангенс — наоборот, косинус делим на синус.
2. Знаки синуса, косинуса, тангенса и котангенса.
3. Синус — функция нечётная, косинус — чётная.
4. Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен 2π.
Графики тригонометрических функций
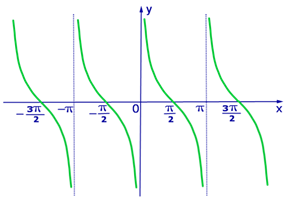
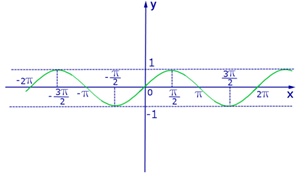
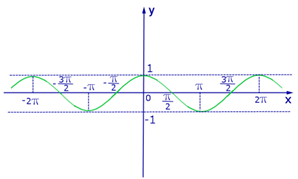
На рисунках приведены графики тригонометрических функций: y = sinx, y = cosx, y = tgx, y = ctgx.
1. График функции y = sinx
2. График функции y = cosx
3. График функции y = tgx
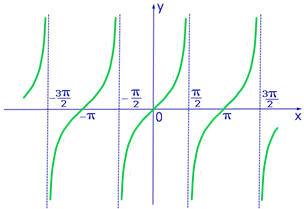
4. График функции y = ctgx