51. Планиметрия
 Читать 0 мин.
Читать 0 мин.
51.364. Окружнoсть
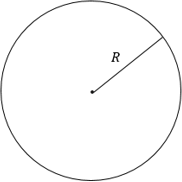
Окружность ― множество всех точек плоскости, равноудаленных от данной точки на плоскости (то есть замкнутая линия).
Круг ― часть плоскости, ограниченная окружностью (то есть площадь).
Элементы окружности:
Центр окружности ― точка O.
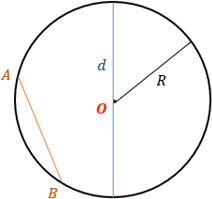
Радиус окружности (r) ― отрезок, соединяющий точку окружности с центром. Все радиусы одной окружности равны.
Диаметр (d) ― хорда, проходящая через центр окружности. Диаметр равен двум радиусам.
Хорда (AB) ― отрезок, соединяющий любые две точки окружности.
Площадь круга и длина окружности:

Дуга и сектор:
|
Дуга окружности — участок окружности между двумя точками на ней. |
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности. |
|
|
|
|
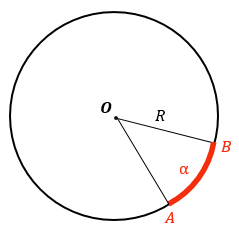
Длина дуги окружности: |
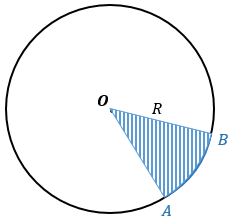
Площадь сектора: |
|
Чтобы найти длину дуги АВ, нужно понять, какую часть она занимает от всей окружности. Это можно сделать через градусную меру дуги (угол между отрезками ОА и ОB). Если окружности — R, а градусная мера дуги АВ — α, то длина всей окружности = 2ℼR, а дуга занимает от всей окружности α/360°. То есть: $l_{AB} = 2\pi R \cdot \displaystyle\frac{\alpha}{360^{\circ}} = \frac{\pi\alpha R}{180^{\circ}}$ |
Чтобы найти площадь сектора ОАВ, нужно понять, какую часть он занимает от всего круга, что можно сделать через градусную меру дуги АВ. Если окружности — R, а градусная мера дуги АВ — α, то площадь всего круга = πR2, а дуга занимает от всей окружности α/360°. То есть: $S_{OAB} = \pi R^2 \cdot \displaystyle\frac{\alpha}{360^{\circ}} = \frac{\pi\alpha R^2}{360^{\circ}}$ |
Касательная к окружности:
Касательная ― прямая, имеющая с окружностью ровно одну общую точку.
СВОЙСТВА КАСАТЕЛЬНОЙ:
|
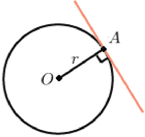
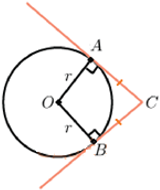
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. |
Отрезки касательных, проведенных из одной точки, равны до точек касания. |
|
|
|
Центральные и вписанные углы:
|
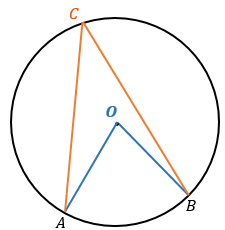
Вписанный угол (ACB) ― угол, вершина которого лежит на окружности, а стороны являются ее хордами |
|
Центральный угол (AOB) ― угол, образованный двумя радиусами: |
|
1. Измеряется половиной дуги, на которую он опирается; 2. Вписанные углы, опирающиеся на одну и ту же дугу, равны; 3. Вписанный угол, опирающийся на диаметр — прямой. |
1. Измеряется дугой, на которую опирается; 2. Центральный угол в два раза больше вписанного, опирающегося на ту же дугу. |
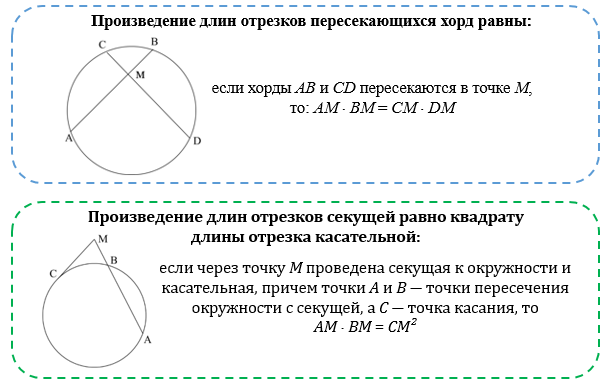
Хорды и секущие: