

40. Алгебра
 Читать 0 мин.
Читать 0 мин.
40.619. Простейшие тригонометрические уравнения
Простейшими тригонометрическими уравнениями называют уравнения вида: sinx = a; cosx = a; tgx = a; ctgx = a, где a – произвольное число.
Решение уравнения sinx = a
|
Обычная форма записи решения |
x = (–1)narcsinα + πn, n є Z |
|
Более удобная форма записи решения |
x1 = arcsinα + 2πn, n є Z x2 = –arcsinα + π + 2πn, n є Z |
|
Ограничения на число a |
В случае, когда α $\notin$ [-1;1], уравнение решений не имеет |
Графическое обоснование решения уравнения sinx = a:
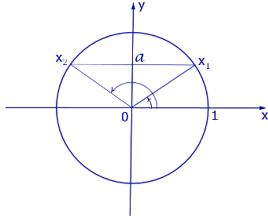
Частные случаи решения уравнений sinx = а
(не учить, а находить по тригонометрическому кругу)
|
Уравнение |
Решение |
|
sinx = 0 |
x = πn, n є Z |
|
sinx = 1 |
x = $\frac{\pi}{2}$ + 2πn, n є Z |
|
sinx = – 1 |
x = –$\frac{\pi}{2}$ + 2πn, n є Z |
Решение уравнения cosx = а:
|
Обычная форма записи решения |
x = ±arccosa + 2πn, n є Z |
|
Более удобная форма записи решения |
x1 = arccosα + 2πn, n є Z x2 = –arccosα + 2πn, n є Z |
|
Ограничения на число a |
В случае, когда α $\notin$ [-1;1], уравнение решений не имеет |
Графическое обоснование решения уравнения cosx = a
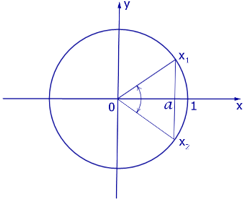
Частные случаи решения уравнений cosx = а
(не учить, а находить по тригонометрическому кругу)
|
Уравнение |
Решение |
|
cosx = – 1 |
x = π + 2πn, n є Z |
|
cosx = 0 |
x = $\frac{\pi}{2}$ + πn, n є Z |
|
cosx = 1 |
x = 2πn, n є Z |
Решение уравнения tgx = а
|
Обычная форма записи решения |
x = arctga + πn, n є Z |
|
Более удобная форма записи решения |
x1 = arctgα + 2πn, n є Z; x2= arctgα + π + 2πn, n є Z |
|
Ограничения на число а |
Ограничений нет |
Графическое обоснование решения уравнения tgx = a
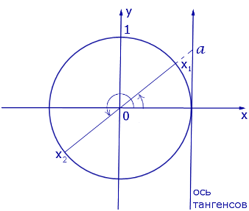
Частные случаи решения уравнений tgx = а
(не учить, а находить по тригонометрическому кругу)
|
Уравнение |
Решение |
|
tgx = 0 |
x = πn, n є Z |
|
tgx = 1 |
x1= $\frac{\pi}{4}$ + 2πn, n є Z x2= $\frac{5\pi}{4}$ + 2πn, n є Z |
|
tgx = – 1 |
x1= –$\frac{\pi}{4}$ + 2πn, n є Z x2= $\frac{3\pi}{4}$ + 2πn, n є Z |
Решение уравнения ctgx = а
|
Обычная форма записи решения |
x = arcctga + πn, n є Z |
|
Более удобная форма записи решения |
x1= arcctgα + 2πn, n є Z x2= arcctgα +π + 2πn, n є Z |
|
Ограничения на число a |
Ограничений нет |
Графическое обоснование решения уравнения ctgx = a
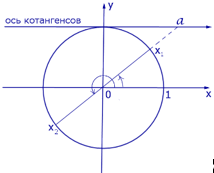
Частные случаи решения уравнений ctgx = а
(не учить, а находить по тригонометрическому кругу)
|
Уравнение |
Решение |
|
ctgx = 0 |
x= $\frac{\pi}{2}$ + πn, n є Z |
|
ctgx = 1 |
x1= $\frac{\pi}{4}$ + 2πn, n є Z x2 = $\frac{5\pi}{4}$ + 2πn, n є Z |
|
ctgx = –1 |
x1= –$\frac{\pi}{4}$ + 2πn, n є Z x2= $\frac{3\pi}{4}$ + 2πn, n є Z |






















