

40. Алгебра
 Читать 0 мин.
Читать 0 мин.
40.691. Метод рационализации
Метод рационализации — это процедура, позволяющая в определённых случаях упростить неравенство и свести его к рациональному неравенству (которое решается методом интервалов).
Позволяет перейти от выражения f к выражению $g$, сохранив все решения.
Метод рационализации для логарифмических неравенств
| Выравнивание $f$ | Выравнивание $g$ |
| $\log_af \vee \log_ag$ | $(a - 1)(f - g)\vee 0 $ |
Здесь мы сравниваем значения относительно друг друга и допускаем случай, когда одно значение больше, а другое меньше и наоборот. Один из способов сравнения двух величин – это вычесть из одного другое. Если разность будет больше нуля, значит, первое число было больше. В первой скобке мы вычитаем из основания единицу. Это значит, что мы сравниваем основание с 1. Во второй скобке мы из одного под логарифмического выражения вычитаем другое, т.е. снова сравниваем их.
Пример. Решите неравенство $\log_{x^2}(x+2) < 1$
Решение.
ОДЗ:
$ \begin{cases} x + 2 > 0 \\ x^2 > 0 \\ x^2 \neq 1 \end{cases} \leftrightarrow \qquad \begin{cases} x > -2 \\ x \neq 0 \\ x \neq \pm 1 \end{cases} $
Преобразуем неравенство
$\log_{x^2} (x + 2) < 1 \\ \log_{x^2}(x + 2) < \log_{x^2}x^2$
Воспользуемся методом рационализации:
$(x^2-1)(x+2-x^2) < 0$
Нам нужно найти такие х, при которых левое выражение меньше правого. В записанном неравенстве, если основание больше единицы, первая скобка будет положительна, и если первое подлогарифмическое выражение будет меньше второго, то их разность будет меньше 0, т.е. вторая скобка будет меньше нуля и это как раз те решения, что нужны нам по условию. Если же основание будет меньше единицы, первая скобка будет отрицательна, что изменит общий знак неравенства. Так же мы действовали, когда писали равносильный переход в виде двух случаев для логарифмического неравенства.
$(x-1)(x+1)(-x^2+x+2)<0 \\ (x-1)(x+1)(x^2-x-2)>0 \\ (x-1)(x+1)(x+1)(x-2) > 0$

С учетом ОДЗ получаем решение неравенства: $x \in (-2; -1) \cup (-1; 0)\cup(0;1)\cup(2; +\infty)$
Ответ: $x \in (-2; -1) \cup (-1; 0)\cup(0;1)\cup(2; +\infty)$
Из рассмотренного метода рационализации вытекают следствия:
| Выравнивание $f$ | Выравнивание $g$ |
| $(\log_af - \log_ag)\cdot h \vee 0$ | $(f - g)\cdot h \vee 0 $ |
| $(\log_fa \vee \log_ga)$ | $(f - 1)(g-1)(a -1)(g -f) \vee 0 $ |
| $(\log_hf \cdot \log_pq) \vee 0$ | $(h - 1)(f-1)(p -1)(q -f) \vee 0 $ |
| $\displaystyle\frac{\log_af - \log_ag}{\log_ap - \log_aq} \vee 0$ | $\displaystyle\frac{f - g}{ p -q} \vee 0$ |
Пример. Решите неравенство: $\log_{12x^2-41x+35}(3-x)\geq\log_{2x^2-5x+3}(3-x)$
Решение.
ОДЗ:
$ \begin{cases} 12x^2-41x+35 > 0, \\ 2x^2-5x+3 > 0, \\ 12x^2-41x+35 \neq 1, \\ 2x^2-5x+3 \neq 1, \\ 3 - x > 0 \end{cases} \leftrightarrow \qquad \begin{cases} (x - \displaystyle\frac{5}{3})(x - \frac{7}{4}) > 0, \\ (x - 1)(x - \displaystyle\frac{3}{2}) > 0, \\ 12x^2 - 41x + 35 \neq 0, \\ 2x^2 - 5x + 2 \neq 0, \\ -x > -3 \end{cases} \leftrightarrow \qquad \begin{cases} (x - \displaystyle\frac{5}{3})(x - \frac{7}{4}) > 0, \\ (x - 1)(x - \displaystyle\frac{3}{2}) > 0, \\ (x - \displaystyle\frac{17}{12})(x - 2) \neq 0, \\ (x - 2)(x - \displaystyle\frac{1}{2}) \neq 0, \\ x < 3 \end{cases} $



$x \in (-\infty; \frac{1}{2}) \cup (\frac{1}{2}; 1)\cup(\frac{3}{2};\frac{5}{3})\cup(\frac{7}{4}; 2)\cup(2; 3)$
Применим метод рационализации:
$(12x^2 - 41x + 35 -1)(2x^2-5x+3-1)(3-x-1)(2x^2-5x+3-(12x^2-41x+35))\geq 0\\ (12x^2-41x+34)(2x^2-5x+2)(-x+2)(-10x^2+36x-32)\geq 0\\ (x - \displaystyle\frac{17}{12})(x-2)(x-2)(x - \frac{1}{2})(-1)(x-2)(-10)(x-2)(x - \frac{8}{5})\geq 0 \\ (x - \displaystyle\frac{17}{12})(x-2)^4(x - \frac{1}{2})(x - \frac{8}{5})\geq 0$

С учетом ОДЗ: $x \in (\frac{1}{2}; 1) \cup [\frac{8}{5}; \frac{5}{3})\cup(\frac{7}{4};2)\cup(2; 3)$
Ответ: $x \in (\frac{1}{2}; 1) \cup [\frac{8}{5}; \frac{5}{3})\cup(\frac{7}{4};2)\cup(2; 3)$
Метод рационализации для неравенств с модулем
| Выравнивание $f$ | Выравнивание $g$ |
| $|f|-|g| \vee 0$ | $f^2-g^2 \vee 0 $ |
| Следствие | |
| $(|f| - |g|)\cdot h \vee 0$ | $ (f^2 - g^2)\cdot h \vee 0 $ |
При сравнении двух чисел по модулю нас не интересует знак числа, поэтому можем от знака избавиться при помощи чётной степени. избавит нас от знака. При дальнейшей работе с полученным неравенством выполнять возведение в квадрат не обязательно, лучше применить формулу разности квадратов.
Пример. Решите неравенство
$|x^2 - 1| - |2x -2| < 0$
Решение. Воспользуемся методом рационализации:
$|x^2-1|-|2x-2| < 0 \\ (x^2-1)^2 - (2x - 2)^2 < 0 \\ ((x^2-1)-(2x-2))((x^2-1)+(2x - 2)) < 0 \\ (x^2 - 1 - 2x +2)(x^2 - 1 + 2x - 2) < 0 \\ (x^2 - 2x +1)(x^2+2x-3)< 0 \\ (x-1)^2(x - 1)(x + 3) < 0$

Решением неравенства является интервал (-3;1)
Ответ: $x \in (-3; 1)$
Пример. Решите неравенство
$|x^2 - 13x + 35| > |35 - x^2|$
Решение. Воспользуемся равносильным переходом:
$(x^2 - 13x + 35)^2 > (35 - x^2)^2, \\ (x^2 - 13x+35-(35-x^2))(x^2-13x+35+(35-x^2))>0, \\ (x^2-13x+35-35+x^2)(x^2-13x+35+35-x^2) > 0, \\ (2x^2-13x)(-13x+70) > 0, \\ -13x(2x-13)(x - \displaystyle\frac{70}{13}) > 0, \\ 2x(x - \displaystyle\frac{13}{2})(x - \frac{70}{13}) < 0, \\ x(x - \displaystyle\frac{13}{2})(x - \frac{70}{13}) < 0, \\ x(x - 6\displaystyle\frac{1}{2})(x - 5\frac{5}{13}) < 0, \\$
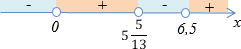
Решением неравенства является промежуток $(-\infty;0) \cup (5\displaystyle\frac{5}{13};6,5).$
Ответ: $x \in(-\infty;0) \cup (5\displaystyle\frac{5}{13};6,5).$
Метод рационализации для иррациональных неравенств
| Выравнивание $f$ | Выравнивание $g$ |
| $\sqrt{f} \vee \sqrt{g}$ | $f \vee g $ |
| Следствие | |
| $(\sqrt{f} - \sqrt{g})\cdot h \vee 0$ | $ (f - g)\cdot h \vee 0 $ |
Пример. Решите неравенство $\displaystyle\sqrt{x^2+5x} < \sqrt{1 - x^2 +4x}$.
Решение.
ОДЗ (находим ОДЗ для меньшего из выражений, ОДЗ для большего выражения выполнится автоматически):
$x^2+5x\geq0, \\ x(x+5)\geq 0, \\ x \in (-\infty; -5] \cup [0; +\infty).$
Воспользуемся методом рационализации:
$x^2 + 5x < 1 - x^2 + 4x, \\ x^2 + 5x - 1 + x^2 -4x < 0, \\ 2x^2 + x -1 < 0, \\ (x+1)(x - 0,5)<0. \\ x \in (-1; 0,5).$
С учетом ОДЗ получаем окончательное решение неравенства: $x \in [0; 0,5).$
Ответ: $x \in [0; 0,5).$
Метод рационализации для показательных неравенств
| Выравнивание $f$ | Выравнивание $g$ |
| $a^f \vee a^g$ | $(a -1)(f-g) \vee 0$ |
| Следствие | |
| $\displaystyle\frac{a^f - a^g}{a^p - a^q} \vee 0$ | $\displaystyle\frac{f -g}{p -q} \vee 0$ |
| $(a^f - a^g)\cdot h \vee 0$ | $(f- g)\cdot h \vee 0$ |
Для показательно-степенных неравенств действуют те же правила, что и для логарифма. При основании, большем 1, знак неравенства мы можем сохранить, при основании меньше единицы, знак неравенства должен измениться при переходе к степеням. Тогда мы можем записать это, как произведение двух скобок, в первой мы будем сравнивать основание с единицей, а во второй – значения показателей степеней.
Пример. Решите неравенство
$x^{x^2+3x-4} < x^{5-x}$
ОДЗ: $x > 0, x \neq 1$
Воспользуемся методом рационализации:
$(x - 1)(x^2+3x -4-(5-x)) <0 \\ (x-1)(x^2+3x-4-5+x) < 0 \\ (x - 1)(x^2 + 4x - 9)< 0 \\ (x - 1)(x - (-2-\sqrt{13}))(x - (-2+\sqrt{13})) < 0$

Видим, что решением является промежуток: $(-\infty; -2 - \sqrt{13})\cup (1; -2 + \sqrt{13})$
С учетом ОДЗ: $x \in (1; -2 + \sqrt{13})$
Ответ: $x \in (1; -2 + \sqrt{13})$
Сведем все рассмотренные равносильные преобразования в таблицу
| Выравнивание $f$ | Выравнивание $g$ |
| $\log_af \vee \log_ag$ | $(a - 1)(f - g)\vee 0 $ |
| $(\log_af - \log_ag)\cdot h \vee 0$ | $(f - g)\cdot h \vee 0 $ |
| $(\log_fa \vee \log_ga)$ | $(f - 1)(g-1)(a -1)(g -f) \vee 0 $ |
| $(\log_hf \cdot \log_pq) \vee 0$ | $(h - 1)(f-1)(p -1)(q -f) \vee 0 $ |
| $\displaystyle\frac{\log_af - \log_ag}{\log_ap - \log_aq} \vee 0$ | $\displaystyle\frac{f - g}{ p -q} \vee 0$ |
| $|f|-|g| \vee 0$ | $f^2-g^2 \vee 0 $ |
| $(|f| - |g|)\cdot h \vee 0$ | $ (f^2 - g^2)\cdot h \vee 0 $ |
| $\sqrt{f} \vee \sqrt{g}$ | $f \vee g $ |
| $(\sqrt{f} - \sqrt{g})\cdot h \vee 0$ | $ (f - g)\cdot h \vee 0 $ |
| $a^f \vee a^g$ | $(a -1)(f-g) \vee 0$ |
| $\displaystyle\frac{a^f - a^g}{a^p - a^q} \vee 0$ | $\displaystyle\frac{f -g}{p -q} \vee 0$ |
| $(a^f - a^g)\cdot h \vee 0$ | $(f- g)\cdot h \vee 0$ |






















