51. Планиметрия
 Читать 0 мин.
Читать 0 мин.
51.143. Векторы
ОСИ КООРДИНАТ:
Для понимания темы «вектор», надо сначала разобраться с понятием «декартовы координаты».
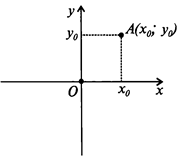
- ось x — ось абсцисс;
- ось y — ось ординат,
- точка О — начало координат.
Любой точке плоскости сопоставляются два числа:
- абсцисса x0,
- ордината y0.
Эти числа называются декартовыми координатами данной точки.
ВЕКТОР:
Вектор — направленный отрезок прямой. То есть это отрезок, для которого указано, какая из его точек является началом, а какая — концом.
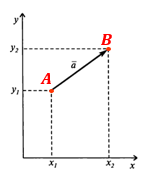
Пусть имеются две точки:
- A с координатами $(x_1;\,y_1)$
- B с координатами $(x_2;\,y_2)$.
Тогда мы имеем вектор $\,\overline {\!AB\,}$, который обозначим за $\overline a.$
На примере вектора рассмотрим основные понятия, связанные с векторами.
Во-первых, для каждого вектора можно найти его координаты и модуль.
КООРДИНАТЫ ВЕКТОРА И МОДУЛЬ ВЕКТОРА:
Координаты вектора — разности координат конца и начала вектора. На примере вектора $\overline a$ его координатами будут: $(a_x;\,a_y).$ Свойства координат вектора:
- Координаты вектора не изменяются при параллельном переносе.
- У равных векторов соответствующие координаты равны.
Нахождение координат вектора:
Координаты вектора $\overline a\;(a_x;\,a_y)\colon$
$\begin{aligned}&a_x=x_2-x_1\\&a_y=y_2-y_1\end{aligned}$
То есть, координаты вектора $\overline a\colon (x_2-x_1;\,y_2-y_1;\,z_2-z_1).$
Модуль вектора — длина вектора (обозначается ). Находится как квадратный корень из суммы квадратов координат вектора.
$|\overline a|=\sqrt{(a_x)^2+(a_y)^2\vphantom{\bigl(}}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2\vphantom{\bigl(}}$
Если рассмотреть пространственный вектор, то в эти формулы добавляется третья координата — z.
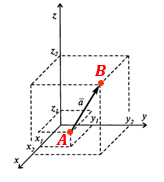
Координаты вектора $\overline a\;(a_x;\,a_y;\,a_z)$:
$\begin{aligned}&a_x = x_2-x_1 \\ &a_y = y_2-y_1 \\ &a_z = z_2 - z_1\end{aligned}$
То есть, координаты вектора $\overline a\colon (x_2-x_1;\,y_2-y_1;\,z_2-z_1).$
Модуль вектора $\overline a\colon$
$|\overline a|=\sqrt{(a_x)^2+(a_y)^2+(a_z)^2\vphantom{\bigl(}}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2\vphantom{\bigl(}}$
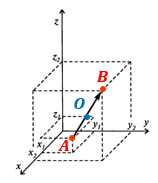
СЕРЕДИНА ВЕКТОРА:
Чтобы найти середину вектора по координатам нужно:
1. Вычислить сумму координат начала и конца вектора.
2. Разделить на два.
|
НА ПЛОСКОСТИ |
В ПРОСТРАНСТВЕ |
|
O — середина вектора $\,\overline {\!AB\,}$ |
|
|
|
|
|
$\begin{aligned}&A\,(x_1;\,y_1),\ B\,(x_2;\,y_2) \\[3pt] &O(x;y)=\left(\frac{x_1+x_2}{2};\,\frac{y_1+y_2}{2}\right)\end{aligned}$ |
$\begin{aligned}&A\,(x_1;\,y_1;\,z_1),\ B\,(x_2;\, y_2;\, z_2) \\[3pt] &O(x;y;z)=\left(\frac{x_1+x_2}{2};\,\frac{y_1+y_2}{2};\,\frac{z_1+z_2}{2}\right)\end{aligned}$ |
ВИДЫ ВЕКТОРОВ:
Единичный вектор — вектор, длина которого равна 1.
Нулевой вектор — отдельные точки плоскости. У такого вектора конец и начало совпадают, а его длина (его модуль) равен нулю.
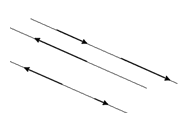
Коллинеарные и компланарные векторы
|
Коллинеарные векторы — векторы, которые параллельны одной прямой или которые лежат на одной прямой.
Два коллинеарных вектора $|\overline a|\ и\ |b|$ называются сонаправленными только тогда, когда их направления соответствуют друг другу: $|\overline a|{\small \uparrow\uparrow}|\overline b|$ |
Компланарные векторы — векторы, которые параллельны одной плоскости или которые лежат на общей плоскости.
В любое мгновение существует плоскость одновременно параллельная двум любым векторам, поэтому два произвольных вектора являются компланарными. |
АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД ВЕКТОРАМИ:
| НА ПЛОСКОСТИ | В ПРОСТРАНСТВЕ | |
| Координаты вектора $\overline {c\,}$ |
Сложение векторов: $\overline {c\,}=\overline a + \overline b$ |
|
| $x$ | $c_x = a_x + b_x$ | $c_x = a_x + b_x$ |
| $y$ | $c_y = a_y + b_y$ | $c_y = a_y + b_y$ |
| $z$ | — | $c_z = a_z + b_z$ |
| Координаты вектора $\overline {c\,}$ |
Вычитание векторов: $\overline {c\,}=\overline a - \overline b$ |
|
| $x$ | $c_x = a_x - b_x$ | $c_x = a_x - b_x$ |
| $y$ | $c_y = a_y - b_y$ | $c_y = a_y - b_y$ |
| $z$ | — | $c_z = a_z - b_z$ |
| Координаты вектора $\overline {b}$ |
Умножение вектора на число: $\overline b = \lambda\overline a$ |
|
| $x$ | $\overline b_x = \lambda a_x$ | $\overline b_x = \lambda a_x$ |
| $y$ | $\overline b_y = \lambda a_y$ | $\overline b_y = \lambda a_y$ |
| $z$ | — | $\overline b_z = \lambda a_z$ |
| Значение числа $s$ | Скалярное умножение векторов: $s = \overline a\cdot\overline b$ |
|
| $s=a_x\!\cdot b_x + a_y\!\cdot b_y$ | $s=a_x\!\cdot b_x + a_y\!\cdot b_y + a_z\!\cdot b_z$ | |
ГЕОМЕТРИЧЕСКОЕ СЛОЖЕНИЕ И ГЕОМЕТРИЧЕСКАЯ РАЗНОСТЬ ВЕКТОРОВ:
СЛОЖЕНИЕ
Сумма двух векторов находится с помощью правила треугольника или правила параллелограмма: $\overline {c\,} = \overline a + \overline b$.
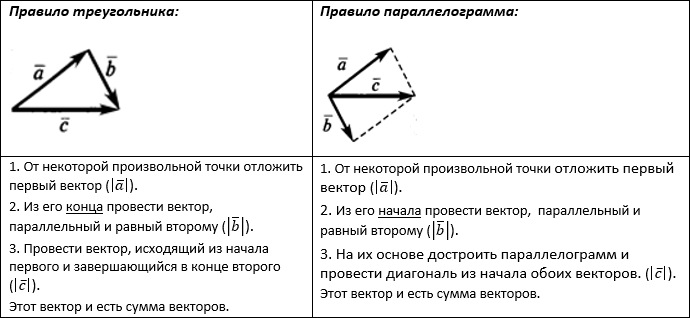
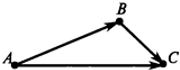
${\mathbf {Теорема\colon}}\\ Для\ любых\ трёх\ точек\ A,\,B,\,C\ справедливо\ соотношение\colon\ \overline{\!AB\,}+\,\overline{\!BC\,}=\,\overline{\!AC\,}\!.$
${\mathbf {РАЗНОСТЬ}}\\Разность\ двух\ векторов\ \overline a\ и\ \overline b\;—\ это\ вектор\ \overline {c\,},\ который\ в\ сумме\ с\ вектором\ \overline b\ даёт\ вектор\ \overline a \\ \overline b + \overline{c\,} = \overline a\quad\Rightarrow\quad\overline{c\,} = \overline a - \overline b$

$Вектор\ \overline {c\,}\ можно\ найти\ также,\ складывая\ с\ вектором\ \overline a\ вектор\ \bigl(-\overline b\bigr),\ противоположный\ вектору\ \overline b\colon \\ \overline {c\,} = \overline a + \bigl(-\overline b\bigr)$