Определение

Модуль числа а или абсолютная величина числа а равна а, если а больше или равно нулю и равна −а, если а меньше нуля:

$|a|=\left\{\begin{aligned}&a,&\hskip-10pt если\ a\ge0; \\ &-a,&\hskip-10pt если\ a<0. \end{aligned}\right.$

Из определения следует, что для любого действительного числа а, │а│ ≥ 0.

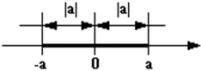
Геометрически │а│ означает расстояние на координатной прямой от точки, изображающей число а, до начала отсчета.

Если а ≠ 0, то на координатной прямой существует две точки а и −а, равноудаленной от нуля, модули которых равны.

Если а = 0, то на координатной прямой │а│изображается точкой 0.

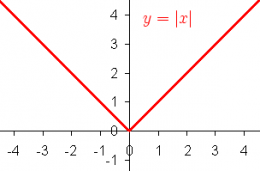
Графиком функции y = │x│ является «уголок».

I) Уравнения вида │f (x) │ = A, A ϵ R решаются следующим образом:

Если A < 0, то корней нет.

Если A = 0, то уравнению │f (x) │ = A соответствует уравнение f (x) = 0.

Если A > 0, то уравнению │f (x) │ = A соответствует равносильная совокупность:

$\left[\begin{aligned}&f(x)=A\\&f(x)=-A\end{aligned}\right.$

II) Уравнения вида │f (x)│ = g (x) решаются следующим образом:

Способ №1

Уравнению │f (x)│ = g (x) соответствует равносильная совокупность систем:

$\left[\begin{aligned} &\left\{\begin{aligned} &g(x)\ge0\\ &f(x)=g(x) \end{aligned}\right.\\ &\left\{\begin{aligned} g(x)&\ge0\\ -f(x)&=g(x)\\ \end{aligned}\right.\\ \end{aligned} \right.$

Способ №2

Уравнению │f (x) │ = g (x) соответствует равносильная совокупность систем:

$\left[\begin{aligned} &\left\{\begin{aligned} &f(x)\ge0\\ &f(x)=g(x) \end{aligned}\right.\\ &\left\{\begin{aligned} f(x)&\ge0\\ -f(x)&=g(x)\\ \end{aligned}\right.\\ \end{aligned} \right.$

III) Уравнения вида │f (x) │ = │g (x) │ решаются следующим образом:

Способ №1

Уравнению │f (x) │ = │g (x) │ соответствует равносильное уравнение f² (x) = g² (x).

Способ №2

Уравнению │f (x)│ = │g (x) │ соответствует равносильная совокупность:

$\left[\begin{aligned}&f(x)=g(x)\\&f(x)=-g(x)\end{aligned}\right.$

IV) Уравнения вида │f (x) │ = −f (x) и │f (x) │ = f (x) решаются следующим образом:

Уравнению │f (x) │ = −f (x) соответствует равносильное неравенство f (x) ≤ 0.

Уравнению │f (x) │ = f (x) соответствует равносильное неравенство f (x) ≥ 0.

V) Общая схема решения уравнений содержащих знак модуль.

Например:

│x² − 1│ + │x² − 4│ = 3.

Найдем нули выражений, стоящих под знаком модуль.

x = ±1, x = ±2.

И раскроем модуль на каждом из 5 промежутков, на которые оказалась разделена числовая ось числами x = ±1, x = ±2.

I) $\left\{\begin{aligned}&x\le-2\\&x^2-1+x^2-4=3\end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&x\le-2\\&x=\pm2\end{aligned}\right.$

(−∞; −2] — промежуток, значит в ответ попадает только решение x = −2.

II) $\left\{\begin{aligned}&-2< x<-1\\&x^2-1-x^2+4=3\end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&-2< x<-1\\&3=3,\ верно\end{aligned}\right.$

В ответ будет входить весь промежуток.

III) $\left\{\begin{aligned}&-1\le x\le1\\&-x^2+1-x^2+4=3\end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&-1\le x\le1\\&x=\pm1\end{aligned}\right.$

Оба решения попадают в рассматриваемый промежуток.

IV) $\left\{\begin{aligned}&1< x<2\\&x^2-1-x^2+4=3\end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&1< x<2\\&3=3,\ верно\end{aligned}\right.$

В ответ будет входить весь промежуток.

V) $\left\{\begin{aligned}&x\ge2\\&x^2-1+x^2-4=3\end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&x\ge2\\&x=\pm2\end{aligned}\right.$

[2; +∞) — промежуток, т. е. подходит решение x = 2.

Ответ: $[-2;-1]\cup[1;2]$.