61. Стереометрия
 Читать 0 мин.
Читать 0 мин.
61.107. Углы
Углы
Классическим заданием с развернутым ответом на стереометрию является задача на нахождение угла. В стереометрии найти угол могут предложить между следующими комбинациями фигур:

Рассмотрим каждую комбинацию, чтобы понять, как искать разные виды углов и какие методы можно применять.
УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Угол между скрещивающимися прямыми ― это угол между параллельными им прямыми, лежащими в одной плоскости.
Это значит, что никогда не пересекающиеся прямые в пространстве мы делаем «пересекающимися»: для этого нужно построить пересекающиеся прямые, параллельные данным. Угол между ними будет искомым.
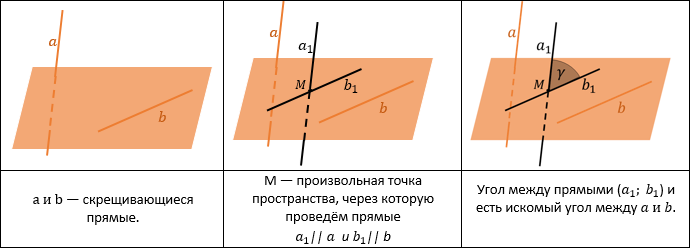
Часто достаточно только к одной из скрещивающихся прямых построить параллельную прямую.
Например, если бы мы отметили точку M на прямой b и через точку M провели прямую $ a_1 \parallel a $.
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Угол между прямой и плоскостью - угол между прямой и ее проекцией на эту плоскость.
Для того, чтобы найти угол между прямой и плоскостью, нужно сначала получить проекцию этой прямой на плоскость, а потом найти угол.
|
|
|
|
|
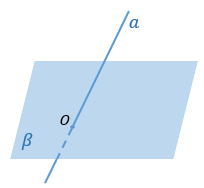
Прямая, пересекающая плоскость β в точке O |
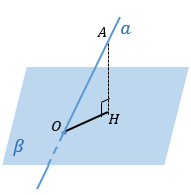
Из произвольной точки А на прямой опустим перпендикуляр AH на плоскость β. Тогда OH – проекция прямой на плоскость β. |
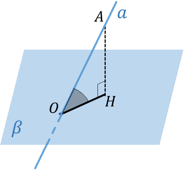
Угол между прямой и наклонной, то есть ∠ AOH и есть искомый угол между . |
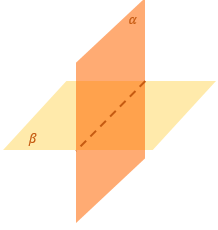
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Для начала вспомним пару определений:
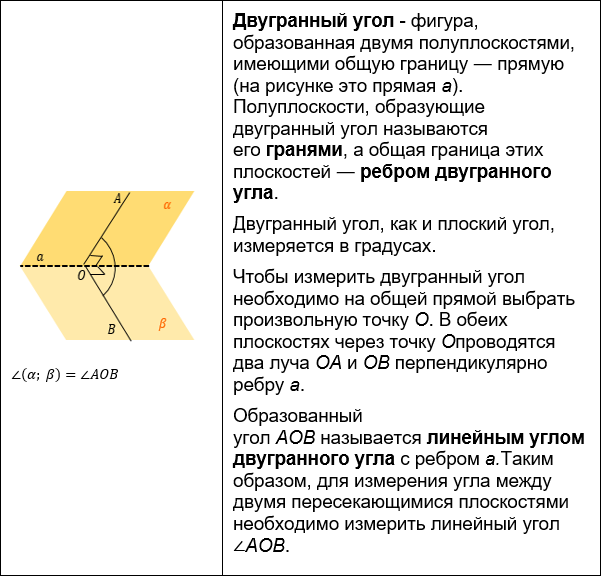
Метод перпендикуляров к линии пересечения.Нахождения угла между плоскостями – одна из самых сложных задач на углы, поэтому тут мы можем воспользоваться несколькими методами.
Угол между плоскостями вычисляется как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения. Это основной способ нахождения угла между плоскостями.
|
|
|
|
|
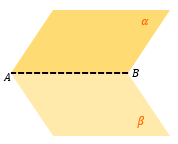
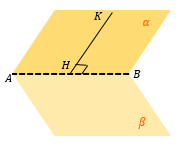
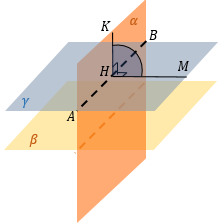
Находим линию пересечения плоскостей α и β – AB. |
Из «удобной» точки К в плоскости α (это может быть вершина многогранника, середина ребра и т.д.) опускаем перпендикуляр KH на AB. |
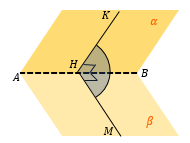
В точку H опустим перпендикуляр из точки M в плоскости β. ∠ KHM – искомый угол между плоскостями α и β |
- Метод перпендикуляров к плоскостям.
Угол между плоскостями вычисляется как угол между перпендикулярами к данным плоскостям. Этот способ удобен, если перпендикуляр к плоскости построить удобнее, чем построить перпендикуляры к линии пересечения плоскостей (или перпендикуляр к плоскости уже есть по условию задачи).
|
|
|
|
|
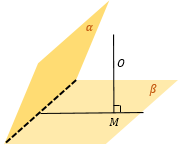
Из произвольной точки O пространства опустим перпендикуляр OM на плоскость β. |
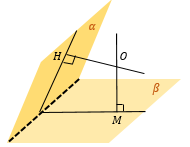
Из точки O опустим так же перпендикуляр OH на плоскость α. |
Любой из двух смежных углов между OM и OH может считать искомым, но так как угол между плоскостями измеряется от 0 до 90°, то берем острый. ∠ MOK – искомый угол между плоскостями α и β |
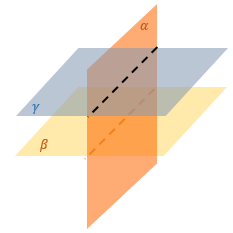
- Метод параллельных плоскостей.
Угол между плоскостями вычисляется как угол между плоскостями, параллельными данным плоскостям. Этот способ применим, когда угол между данными плоскостями по каким-то причинам искать неудобно, а удобнее найти угол между плоскостями, параллельными данным.
|
|
|
|
|
Угол между плоскостями α и β затруднительно искать (например, нет «удобных точек» или тяжело построить взаимные перпендикуляры). |
Построим плоскость γ, параллельную β (или в стереометрической фигуре она уже есть) |
По методу перпендикуляров к линии пересечения найдем угол между плоскостями α и γ. ∠ MНK – искомый угол между плоскостями α и β |