40. Алгебра
 Читать 0 мин.
Читать 0 мин.
40.659. Отбор корней
Задача 1
а) Решите уравнение: sinx = 0,5.
б) Укажите корни, принадлежащие отрезку [-π; 2π].
Решение:
а) sinx = 0,5;
х = $\frac{\pi}{6}$ + 2πn или x = 5 · $\frac{\pi}{6}$ + 2πk, n, k $\in$ Z.
Корни уравнения: $\frac{\pi}{6}$ + 2πn, 5 · $\frac{\pi}{6}$ + 2πk, k $\in$ Z.
б) Теперь будем искать корни, принадлежащие отрезку [-π; 2π].
Рассмотрим 3 способа отбора корней:
- Способ №1. С помощью двойного неравенства:
−π ≤ $\frac{\pi}{6}$ + 2πn ≤ 2π;
−1 ≤ $\frac{1}{6}$ + 2n ≤ 2;
$-\frac{7}{6}$ ≤ 2n ≤ $\frac{11}{6}$
$-\frac{7}{12}$ ≤ n ≤ $\frac{11}{12}$.
Значит, n = 0, x = $\frac{\pi}{6}$.
−π ≤ 5 · $\frac{\pi}{6}$ + 2πk ≤ 2π;
−1 ≤ $\frac{5}{6}$ + 2k ≤ 2;
−$\frac{11}{6}$ ≤ 2k ≤ $\frac{7}{6}$;
−$\frac{11}{6}$ ≤ k ≤ -$\frac{7}{12}$.
Значит, k = 0, х = 5 · $\frac{\pi}{6}$.
Этот способ наиболее точный и если учащиеся владеют навыками решения двойного неравенства, то понятный и подходит совершенно всем и в любых случаях.
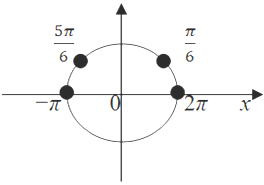
- Способ №2. С помощью окружности:
a) На окружности найдем края отрезка: точки –π и 2π.
б) Смотрим на точки — из каких серий решения попали в этот отрезок.
в) Выбираем эти точки.
Если данные отрезки бывают длиной больше 2π, тогда можно потерять некоторые корни, поэтому рекомендуется: нарисовать вторую концентрическую окружность, будто соответствующую следующему периоду (это просто модель, которая помогает решить задачу). Этот способ хорошо дается тем, кто умеет определять на окружности точки и отсчитывать периоды.
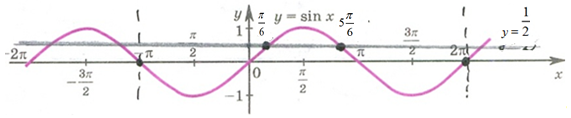
- Способ №3. С помощью графика:
а) Чертим график у = sinx;
б) Выделяем отрезок —π; 2π;
в) Проводим прямую у = $\frac{1}{2}$;
г) Отмечаем точки с ординатой $\frac{1}{2}$ на искомом отрезке, получаем х = $\frac{\pi}{6}$ и 5 · $\frac{\pi}{6}$.
Способ очень наглядный и подойдет тем, кто не усвоил вышеизложенные два способа.